Операции над нечеткими множествами. Подчеркнем, что нечеткие множества являются обобщением обычных четких множеств

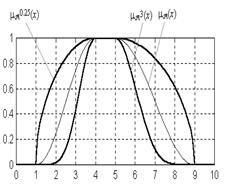
Подчеркнем, что нечеткие множества являются обобщением обычных четких множеств. Поэтому любое определение некоторой операции над нечеткими множествами должно быть справедливым в случае, когда вместо нечетких множеств используются обычные множества. Для обеспечения возможности сравнения нечетких множеств и выполнения над ними различных операций соответствующие нечеткие множества должны быть определены на одном и том же универсуме.

Прежде всего, определим следующие два простейших отношения между нечеткими множествами.

Равенство. Два нечетких множества A={x, mA(x)} и B={x, m_B(x)} считаются равными (A=B), если их функции принадлежности принимают равные значения на универсуме X:

m_A(x)= m _B (x) для любого xÎX. (1.1)

Нечеткое подмножество. Нечеткое множество A={ x, m_A(x)} является нечетким подмножеством нечеткого множества B={ x, m_B(x)} (обозначают AÍB) тогда и только тогда, когда выполняется следующее условие:

m_A(x)£ m_B(x) (" x Î X). (1.2)

Говорят, что нечеткое множество B доминирует нечеткое множество A, а нечеткое множество A содержится в нечетком множестве B. Нечеткое множество A называют также несобственным подмножеством множества B.

Если в определении нечеткого подмножества исключается равенство соответствующих нечетких множеств, то A называется собственным нечетким подмножеством B и обозначается: AÌ B. При этом нечеткое множество B строго доминирует нечеткое множество A, а нечеткое множество A строго содержится в нечетком множестве B.

Приведем определения нескольких важных логических операций над нечеткими множествами.

Пересечением двух нечетких множеств A и B называют нечеткое множество С (C=AÇB), заданное на этом же универсуме X, функция принадлежности которого определяется по формуле:

m_С(x)= min{m_A(x),m_B(x)} (" x Î X). (1.3)

Пересечение AÇB есть наибольшее нечеткое подмножество C, которое содержится одновременно в нечетких множествах A и B.

Операцию пересечения нечетких множеств называют также min-пересечением или Ù-пересечением (по определению логической операции "И", обозначаемой знаком "Ù").

Объединением двух нечетких множеств A и B называют нечеткое множество С (D=AÈB), заданное на этом же универсуме X, функция принадлежности которого определяется по формуле:

m _D(x)= max{m_A(x),m_B(x)} (" x Î X). (1.4)

Объединение AÈB есть наименьшее нечеткое множество D, которое доминирует одновременно A и B. Операцию объединения нечетких множеств называют max- объединением или Ú-объединением (по определению логической операции "ИЛИ", обозначаемой знаком "Ú").

Заметим, что эта же операция в терминах вероятностного подхода задается в виде:

m _D (x)=m _A(x) + m _B(x) – m_A(x) * m _B (x).

Разностью двух нечетких множеств A и B называется некоторое третье нечеткое множество S (обозначается S=A\B), заданное на этом же универсуме X, функция принадлежности которого определяется по формуле:

m_S(x) = max{m_A(x) - m_B (x), 0} (" x Î X), (1.5)

где используется операция арифметической разности двух чисел.

При построении нечетких моделей сложных систем широко используются унарные операции умножения нечеткого множества на число и возведение нечеткого множества в степень.

Умножение нечеткого множества на число. Пусть A={ x, m_A(x)} — произвольное нечеткое множество, заданное на универсуме X; a — положительное действительное число, такое, что a × h _A £1 (h _A — высота нечеткого множества A). Результат операции умножения нечеткого множества A на число a определяется как нечеткое множество B={ x, m_B(x)}, заданное на этом же универсуме X, функция принадлежности которого определяется по формуле:

m_B(x)= a ×m_A(x) (" x Î X). (1.6)

Эту операцию в дальнейшем будем обозначать через a ×A.

Возведение в степень. Пусть A={ x, m_A(x)} — произвольное нечеткое множество, заданное на универсуме X; k — положительное действительное число. В этом случае формально можно определить операцию возведения нечеткого множества A в степень k как нечеткое множество B={ x, m_B(x)}, заданное на этом же универсуме X, функция принадлежности которого определяется по формуле:

m_B(x) = m_A(x) ^k (" x Î X). (1.7)

Примеры графического представления операции возведения нечеткого множества в степень приведены на рис. 1.2.

Рис. 1.2. Представление операций возведения в степень

На основе операции возведения в степень определяются две специальные операции над нечеткими множествами: операция концентрирования и операция растяжения нечеткого множества.

Концентрирование. Пусть на универсуме X задано произвольное нечеткое множество A={ x, m_A(x)}. Операция концентрирования, обозначаемая через CON(A), дает в результате нечеткое множество C={ x, m_C(x)}, функция принадлежности которого:

m_C(x) = m_A(x)² (" x Î X). (1.8)

Очевидно, в этом случае CON(A)=A².

Например, для конечного нечеткого множества A={<1, 1.0>, <2, 1.0>, <3, 0.9>, <4, 0.8>, <5, 0.6>, <6, 0.5>, <7, 0.4>, <8, 0.2>, <9, 0.1>} его концентрирование равно: CON(A)=A²={<1, 1.0>, <2, 1.0>, <3, 0.81>, <4, 0.64>, <5, 0.36>, <6, 0.25>, <7, 0.16>, <8, 0.04>, <9, 0.01>}.

Растяжение. Операция растяжения, обозначаемая через DIL(A), дает в результате нечеткое множество D={ x, m_D(x)}, функция принадлежности которого:

m_D(x) = m_A(x)^0.5 (" x Î X). (1.9)

С помощью операций концентрирования и растяжения выполняется усиление и ослабление лингвистических понятий соответственно. В частности, с помощью операции концентрирования можно задать модификатор «ОЧЕНЬ» для некоторого лингвистического понятия, а с помощью операции растяжения задается модификатор «СРАВНИТЕЛЬНО» или «БОЛЕЕ МЕНЕЕ».

Например, если некоторое понятие, скажем, «старый возраст», определяется как:

A=<x, m_A(x)>, тогда понятие "очень старый возраст" определяется так: CON(A)=A²=<x, m_A(x)²>.