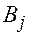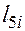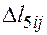Маршрутизация перевозок грузов.
Маршрутизация перевозок – это составление порядка следования п.с. между корреспондирующими пунктами при выполнении перевозок. По одному маршруту могут перевозиться различные грузы, которые удовлетворяют условию возможности и транспортировке одним и тем же п.с. Следовательно, маршрутизации перевозок должно предшествовать выделение из всех грузов, предъявленных к перевозке, групп однородных грузов с точки зрения возможности их перевозки на одном и том же типе п.с. Маршруты составляются отдельно по каждой группе грузов, совпадающих по времени выполнения перевозок. В общем виде задача маршрутизации перевозок формулируется следующим образом: Известны расположение грузоотправителей (ГО) и грузополучателей (ГП), дислокация парка п.с., объемы вывоза и завозов грузов, характеристики транспортной сети и условия движения по ней. Необходимо найти удовлетворяющее определенным требованиям организации транспортного процесса во времени, упорядоченные множества связанных пунктов (АТП, ГО, ГП), представляющие собой маршруты при перевозках на которых достигается экстремальное значение целевой функции – минимум транспортных издержек. Основным содержанием задачи маршрутизации является определение оптимального плана возврата порожних автомобилей, обеспечивающего максимально возможный коэффициент использования пробега и соответственно минимальные транспортные издержки. Объем перевозок из i-го пункта отправления в j-й пункт назначения составляет для k-го груза
где
r – общее число видов перевозимого груза.
Не решая задачи выбора и распределения п.с., будем полагать, что для перевозок используются условные однотонные автомобили. При выполнении перевозок в пункт
приведенных к 1-му классу тонн груза и соответственно прибывает такое же число Х условных автомобилей, которые после разгрузки подаются в пункты погрузки
приведенных к 1-му классу тонн груза, то для пунктов
Кратчайшие расстояния Требуется определить число Данную задачу математически можно записать следующим образом: требуется определить совокупность величин
и минимизирующих функцию
Поскольку количество завозимых грузов равно количеству вывозимых, то справедливо следующее равенство
Сформулированная задача представляет собой классическую транспортную задачу линейного программирования закрытого типа. Подготовку исходных данных для решения поставленной задачи производим в табличной форме (табл.1.3)
Подготовка исходных данных для маршрутизации перевозок грузов. Таблица 1.3
По данным табл.1.3 и формулам (2.) и (3) рассчитываются значения
Сводный план ездок условных однотонных автомобилей для перевозок заданных грузов. Таблица 1.4
Для решения транспортной задачи используют так называемую распределительную таблицу, которая в общем случае имеет ниже приведенный вид (табл.1.5.). Распределительная таблица составляется по данным табл.1.2; 1.3 и 1.4; в нее заносятся расстояния Для отыскания оптимального закрепления ГО с ГП по подаче порожних автомобилей необходимо сделать в распределительной таблице первоначальное закрепление, получить произвольный план закрепления (опорный), удовлетворяющий ограничениям (4), (5), (7) при числе загруженных клеток m+n-1 и отсутствия циклов (контуров). Такой план, содержащий ровно m+n-1 заполненных клеток без циклов, называется базисным. Цикл (контур) в распределительной таблице – это замкнутая ломаная линия, образованная прямыми отрезками, угла между которыми равны 900, а вершины углов лежат в загруженных клетках. Контур может быть четырехугольным, шестиугольным, восьмиугольным и т.д. Если число загруженных клеток – более m+1, то среди них есть цикл. Для получения начального базисного решения (опорного плана) целесообразного применять один из эффективных методов – метод двойного предпочтения. В соответствии с этим методом опорный план составляется по следующему правилу: выбирается минимальное расстояние по каждой строке распределительной таблицы, т.е. находится min клетки в порядке возрастания указанных в них расстояний
где
Из сравниваемых величин Полученное таким образом закрепление является одним из возможных базисных планов. Для оценки оптимальности полученного первоначального базисного плана и (при необходимости) для отыскания оптимального плана закрепления применяется ряд методов: метод квадратов, метод опорных элементов, распределительные методы (метод Хичкока, метод Креко, метод МОДИ), методы с разрешающими элементами. Наиболее широкое применение при ручном счете получил модифицированный распределительный метод (МОДИ). В распределительную таблицу вводятся вспомогательные строки и столбец, в которые вносятся специальные показатели, называемые потенциальными. Метод основан на том, что если к расстояниям любой строки (столбца) распределительной таблицы прибавить или отнять одно и то же произвольное число, то оценка оптимальности относительно не изменится. Если от расстояний каждой i-й строки отнимать число
Принимая для загруженных клеток потенциал для первой строки таблицы принимается равным нулю; по расстояниям загруженных клеток подбираются потенциалы других строк и столбцов таким образом, чтобы соблюдалось принятое условие Затем по вычисленным потенциалом строк Если значение оценочного параметра свободной клетки будет меньше нуля ( Все расчеты сведены в распределительную таблицу (табл.1.5).
Распределительная таблица Таблица 1.5
Как видно из таблицы 1.5, первоначальное базисное решение оказалось оптимальным, так как отсутствуют отрицательные значения оценочного параметра В результате решения поставленной задачи линейного программирования находится оптимальный план возврата порожних автомобилей в пункты отправления груза. По оптимальному сводному плану ездок условных однотонных автомобилей с грузами и оптимальному плану возврата порожних автомобилей составляются рациональные маршруты движения п.с. при перевозке грузов. Составление рациональных маршрутов возможно двумя способами: методом «таблиц связей» и методом «совмещенных планов». Наиболее широкое применение получил последний из них. При использовании данного метода в соответствующие клетки таблицы оптимального сводного плана ездок с грузами (табл.1.4) из таблицы оптимального плана возврата порожних автомобилей переносятся данные, характеризующие число и направление ездок без грузов. Эти цифры выделяются. В тех клетках ij полученой таблицы совмещенных планов, где имеются 2 цифры (выделенная и невыделенная), получаются маятниковые маршруты ездок на которых равно минимуму где
Включенное число в маршрут ездок с грузом или без груза из дальнейшего рассмотрения исключается. Когда все маятниковые маршруты найдены, в таблицы совмещенных планов начинают строить четырехугольные, а затем – шестиугольные и т. д. Контуры, все углы которых лежат в загруженных клетках, причем углы в клетках с гружеными ездками должны чередоваться с углами в клетках с порожними ездками. Каждый из полученных контуров составляет маршрут, число оборотов на котором определяется наименьшим числом в клетках, соответствующих углам контура. Число ездок, включенное в маршрут, при дальнейшем рассмотрении не учитывается. Шифр маршрута состоит из шифров клеток углов контура. Решение ведется до полного исключения всего числа ездок из таблицы совмещенных планов (табл.1.6).
Таблица совмещенного плана ездок с грузом и без груза условный однотонных автомобилей. Таблица 1.6
По данным табл.1.6 составляем сначала маятниковые маршруты с обратным порожним пробегом, а затем – рациональные маршруты путем построения контуров. Разработанные маршруты приведены в табл.1.7 Маршруты перевозок груза Таблица 1.7
После того, как получены маршруты движения при перевозке груза условными однотонными автомобилями, разрабатываются схемы маршрутов перевозки грузов с указанием конкретных видов грузов, объемов их перевозки между каждой парой пунктов фактическое количество k-го груза
где Для каждого маршрута перевозки грузов должно соблюдаться условие
Завершается маршрутизация перевозок грузов решением задачи по закреплению маршрутов за АТП с установлением нулевых пробегов автомобилей. Закрепление маршрутов за АТП требует решение двух взаимосвязанных вопросов: определение начального и соответствующего ему конечного пункта маршрута и непосредственно закрепления маршрута АТП. Начальным пунктом может быть любой ГО, связанный данным маршрутом. При этом выбранному начальному пункту соответствует определенный конечный пункт маршрута. На маятниковых маршрутах с обратным не груженным пробегом имеется только по одному ГО и ГП, поэтому у такого маршрута может быть только один вариант начала и конца. Этого нельзя сказать о других типах маршрута, объединяющих по несколько ГО и ГП. Однако в любом случае устанавливаются возможные варианты начальных и конечных пунктов маршрута, и для каждого варианта определяются расстояния между начальными и конечными пунктами, а также соответствующие ему нулевые пробеги от АТП. Поэтому критерием выбора начального пункта маршрута (первого пункта погрузки) и возвращения его в АТП является оценочный параметр, рассчитываемый по формуле
где
При закреплении маршрутов за АТП рассчитываются значения оценочного параметра для всех возможных вариантов начала выполнения маршрута и по каждому АТП. Из возможных вариантов принимается тот, для которого значение скорректированного нулевого пробега Все расчеты приведены в табл.1.8. Скорректированные нулевые пробеги Таблица 1.8
По модели транспортной сети и данным табл.1.2, 1.7, 1.8 окончательно оформляются схемы маршрутов перевозок грузов с указанием их окончательного шифра и нулевых пробегов (рис.1.2)
|

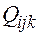 тонн. Указанные объемы перевозок приводятся к одному классу груза. Приведение объемов перевозок грузов к 1-му классу груза производится по следующей формуле:
тонн. Указанные объемы перевозок приводятся к одному классу груза. Приведение объемов перевозок грузов к 1-му классу груза производится по следующей формуле: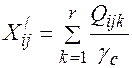 , (1)
, (1)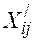 - объем перевозок между пунктами i и j, приведенный к первому классу груза, усл. т.;
- объем перевозок между пунктами i и j, приведенный к первому классу груза, усл. т.;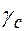 - коэффициент использования грузоподъемности при перевозке k-го груза;
- коэффициент использования грузоподъемности при перевозке k-го груза;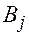 доставляется
доставляется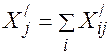 (2)
(2)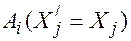 . Так как из пунктов
. Так как из пунктов 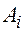 нужно вывезти
нужно вывезти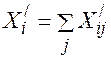 (3)
(3)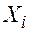 подач порожних условных автомобилей
подач порожних условных автомобилей 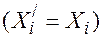 .
.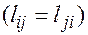 от каждого потребителя
от каждого потребителя 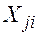 подач порожних однотонных условных автомобилей от j-го пункта разгрузки в i –ый пункт погрузки с тем, чтобы общий пробег автомобилей был минимальный.
подач порожних однотонных условных автомобилей от j-го пункта разгрузки в i –ый пункт погрузки с тем, чтобы общий пробег автомобилей был минимальный.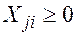 (план возврата порожних автомобилей), удовлетворяющих ограничением.
(план возврата порожних автомобилей), удовлетворяющих ограничением.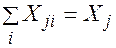 ; (4)
; (4)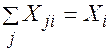 (5)
(5)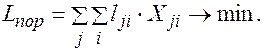 (6)
(6)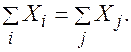 (7)
(7)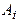
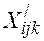

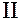
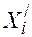 и
и 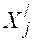 , которые равны числу ездок по возврату порожних условных однотонных автомобилей
, которые равны числу ездок по возврату порожних условных однотонных автомобилей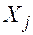 . Их расчет сводится в табл.1.4, являющуюся сводным планом ездок с грузом условных однотонных автомобилей.
. Их расчет сводится в табл.1.4, являющуюся сводным планом ездок с грузом условных однотонных автомобилей.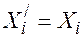
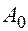
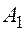
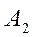
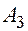
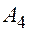
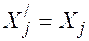
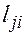 , число отправляемых условных однотонных автомобилей
, число отправляемых условных однотонных автомобилей 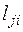 . Такие клетки отмечаются значком, - например, звёздочкой (*). Если в одной строке несколько клеток имеют одинаковые минимальные расстояния, то отмечаются все эти клетки. То же самое проделывается по каждому столбцу, т.е. находятся и отмечаются клетки min
. Такие клетки отмечаются значком, - например, звёздочкой (*). Если в одной строке несколько клеток имеют одинаковые минимальные расстояния, то отмечаются все эти клетки. То же самое проделывается по каждому столбцу, т.е. находятся и отмечаются клетки min 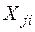 , начиная с отмеченных дважды и последовательно переходя к отмеченным один раз и неотмеченным, пока не будут удовлетворены ограничения (3) и (4). Объём перевозки груза
, начиная с отмеченных дважды и последовательно переходя к отмеченным один раз и неотмеченным, пока не будут удовлетворены ограничения (3) и (4). Объём перевозки груза  , определяется как минимум от числа ездок по строке и по столбцу с учётом ранее назначенных других перевозок:
, определяется как минимум от числа ездок по строке и по столбцу с учётом ранее назначенных других перевозок: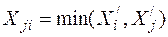 , (8)
, (8)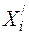 - число порожних ездок к i-му отправителю с учётом ранее назначенных подач от других, кроме j-го, получателей;
- число порожних ездок к i-му отправителю с учётом ранее назначенных подач от других, кроме j-го, получателей;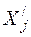 - число порожних ездок от j-го получателя с учётом ранее назначенных перевозок к другим, кроме i-го, отправителям.
- число порожних ездок от j-го получателя с учётом ранее назначенных перевозок к другим, кроме i-го, отправителям.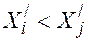 ) либо столбца (если
) либо столбца (если 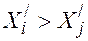 ) полностью исключаются из дальнейшего рассмотрения, а значимая разность соответственно (
) полностью исключаются из дальнейшего рассмотрения, а значимая разность соответственно (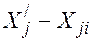 ) или (
) или (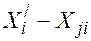 ) подлежит дальнейшему распределению по клеткам таблиц. Если
) подлежит дальнейшему распределению по клеткам таблиц. Если 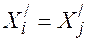 , то оставляется к рассмотрению i-я строка с нулевым либо j-й столбец с нулевым ограничением. Оставляют столбец или строку с меньшими значениями расстояний в клетках, куда может попасть нулевая загрузка. В дальнейшем этой нулевой загрузкой оперируют как значимой положительной величиной.
, то оставляется к рассмотрению i-я строка с нулевым либо j-й столбец с нулевым ограничением. Оставляют столбец или строку с меньшими значениями расстояний в клетках, куда может попасть нулевая загрузка. В дальнейшем этой нулевой загрузкой оперируют как значимой положительной величиной.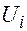 и от расстояний каждого j-го столбца –
и от расстояний каждого j-го столбца – 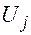 , то тогда относительной оценкой любой клетки ji может служить параметр
, то тогда относительной оценкой любой клетки ji может служить параметр 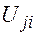 вместо
вместо 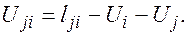 (9)
(9) , то есть расстояние в каждой загруженной клетке должно быть равно сумме потенциалов строки и столбца данной клетки.
, то есть расстояние в каждой загруженной клетке должно быть равно сумме потенциалов строки и столбца данной клетки.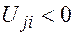 ), то это значит, что перераспределение корреспонденций по клеткам таблицы с занесением загрузки в такую свободную клетку, называемую потенциальной, уменьшит значение целевой функции. Отсутствие клеток с параметром
), то это значит, что перераспределение корреспонденций по клеткам таблицы с занесением загрузки в такую свободную клетку, называемую потенциальной, уменьшит значение целевой функции. Отсутствие клеток с параметром 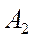
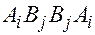 , число
, число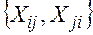 ,
, – число ездок с грузом из
– число ездок с грузом из 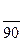
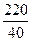

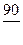
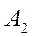
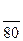
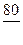
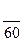
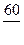
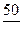
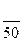
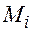
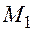
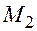
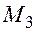
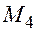
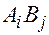 , порожних пробегов от пунктов разгрузки в пункты погрузки. При этом
, порожних пробегов от пунктов разгрузки в пункты погрузки. При этом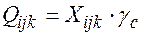 , (10)
, (10)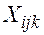 - число ездок с k-м грузом условных однотонных автомобилей между пунктами
- число ездок с k-м грузом условных однотонных автомобилей между пунктами 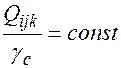 . (11)
. (11) , (12)
, (12)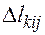 - скорректированный нулевой пробег, км.;
- скорректированный нулевой пробег, км.;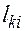 - расстояние от АТП до первого пункта погрузки, км.;
- расстояние от АТП до первого пункта погрузки, км.;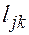 - расстояние от конечного пункта выгрузки до АТП, км.;
- расстояние от конечного пункта выгрузки до АТП, км.;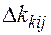 является минимальным, т. е.
является минимальным, т. е. 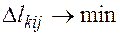 .
.