Задание Б.
В этом задании балка из сосны нестандартного поперечного сечения (прямоугольник, квадрат или круг): необходимо определить площадь этого поперечного сечения А. Рассчитываем из условия прочности[14] при изгибе момент сопротивления изгибу
где
Для плоского прямоугольного сечения осевой момент сопротивления [15] относительно центральной его оси Приравняем расчётное значение
Выразив
Если задано квадратное сечение (приложение 9), то площадь Если в сечении круг (приложение 9), то: В заключение работы необходимо сделать вывод, где указать опасные поперечные сечения[16] по длине балок и для этих сечений расчётные значения
Литература
1. Давыдов Г.А. Конспект лекций по курсу «Сопротивление материалов». – Ленинград: ЛВИМУ им.адм.С.О.Макарова, 1986. – 201 с. 2. Иосилевич Г.Б. Прикладная механика. – М.: Высшая школа. 1989. – 352 с. 3. Стёпин П.А. Сопротивление материалов. – Изд. 8-е. – М.: Высш. Шк., 1988. – 360 с. 4. Тимошенко C.П. Сопротивление материалов. Элементарная теория и задачи. – М.: ФИЗМАТГИЗ, 1960. – 379 с. 5. Федосеев В.И. Сопротивление материалов. – М.: Изд. «Наука». 1974. – 559 с.
|

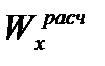 :
: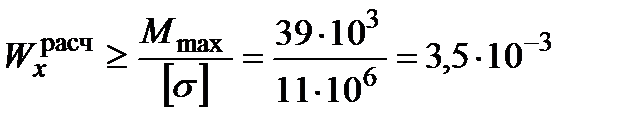 (м3)
(м3)  (см3),
(см3), , см3 – расчётный момент сопротивления изгибу;
, см3 – расчётный момент сопротивления изгибу;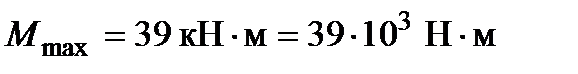 – максимальный изгибающий момент из эпюры Э.М.(рис.1) (самое опасное сечение);
– максимальный изгибающий момент из эпюры Э.М.(рис.1) (самое опасное сечение); – допускаемое нормальное растягивающее напряжение для сосны.
– допускаемое нормальное растягивающее напряжение для сосны.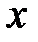 равен (прил. 9)
равен (прил. 9) 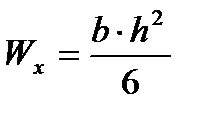 .
. предыдущему выражению:
предыдущему выражению: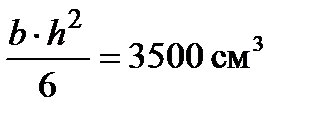
 через
через  (соотношение
(соотношение  (см2).
(см2). рассчитывается аналогично прямоугольному сечению при условии:
рассчитывается аналогично прямоугольному сечению при условии: 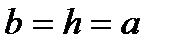 .
.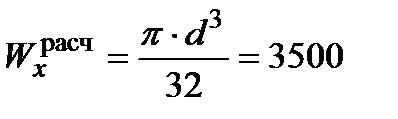 см3. Отсюда находим диаметр балки
см3. Отсюда находим диаметр балки  и определяем площадь поперечного сечения:
и определяем площадь поперечного сечения:  .
. и
и 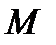 ; имеются ли в заданиях участки с чистым изгибом[17]; исходя из заданных профилей поперечных сечений балок в заданиях, проанализировать, как выгоднее положить балки, чтобы обеспечить максимальную её прочность: положить, как изображено в задании, или повернуть их на 90° (критериями оценки выбора могут служить осевые моменты сопротивления и условия прочности при изгибе).
; имеются ли в заданиях участки с чистым изгибом[17]; исходя из заданных профилей поперечных сечений балок в заданиях, проанализировать, как выгоднее положить балки, чтобы обеспечить максимальную её прочность: положить, как изображено в задании, или повернуть их на 90° (критериями оценки выбора могут служить осевые моменты сопротивления и условия прочности при изгибе).


