ЗАДАЧА I
Построение эпюр
Под действием внешних силовых факторов и опорных реакций балка будет находиться в равновесии. Пренебрегая силами тяжести масс самой балки, из условий равновесия найдём опорные реакции 1. Составим уравнения статики[6] равновесия внешних изгибающих моментов
Отсюда:
Подставив в эти выражения числовые значения заданных величин, найдём реакции: В нашем примере обе реакции положительны, значит их направления выбраны, верно [7].. 2. Производим проверку вычисленных значений
Отметим, что заданный внешний момент Мы не ошиблись в расчётах: силы реакций вычислены, верно. Такую проверку необходимо производить, так как ошибка в определении опорных реакций неминуемо приведёт к ошибкам в построении эпюр. 3. Чтобы построить эпюры При вычислении внутренних поперечных сил Внутренняя перерезывающая сила
принимается положительной, если равнодействующая этих внешних сил слева от рассматриваемого сечения направлена вверх, а справа от рассматриваемого сечения вниз и отрицательной – в противоположном случае. Внутренний изгибающий момент
считается положительным, если в рассматриваемом сечении балка изгибается выпуклостью вниз и отрицательным, если он изгибает балку в сечении выпуклостью вверх. Составим аналитическое выражение (1) в общем виде (с учётом принятого правила знаков) внутренних поперечных сил
|

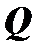 и
и 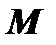
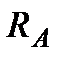 и
и 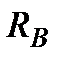 , вызванные заданными нагрузками и определим их действительное направление.
, вызванные заданными нагрузками и определим их действительное направление. относительно опоры
относительно опоры 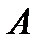 и затем относительно опоры
и затем относительно опоры  :
: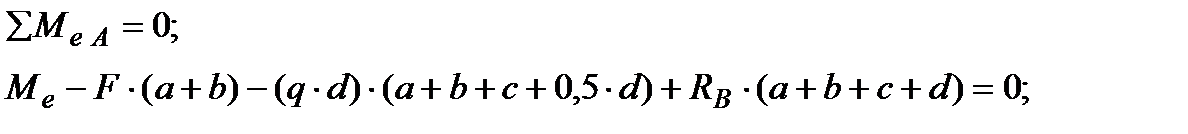
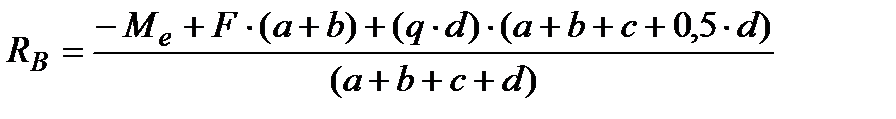 .
.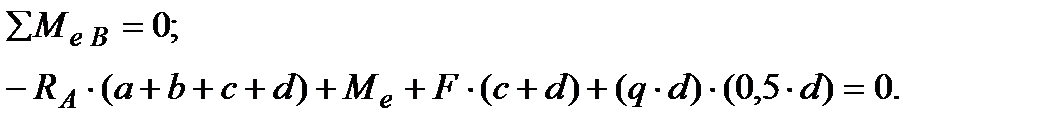

 .
.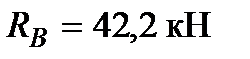 и
и 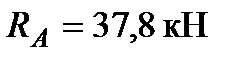 .
. и
и 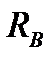 :
: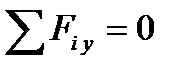 .
.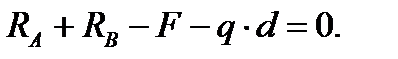
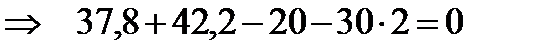 ;
; 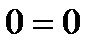 – тождество.
– тождество. входит только в уравнение моментов.
входит только в уравнение моментов. и
и 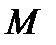 , пользуясь известным в сопротивлении материалов методом сечений, рассчитаем их числовые значения во всех последовательно проведённых поперечных сечениях балки по всей её длине. Для чего рассмотрим произвольные сечения I–I, II–II, III–III и IV–IV (рис.1) с переменными аргументами
, пользуясь известным в сопротивлении материалов методом сечений, рассчитаем их числовые значения во всех последовательно проведённых поперечных сечениях балки по всей её длине. Для чего рассмотрим произвольные сечения I–I, II–II, III–III и IV–IV (рис.1) с переменными аргументами 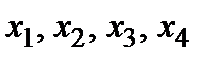 в пределах каждого грузового участка
в пределах каждого грузового участка 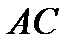 ,
, 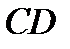 ,
, 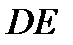 ,
, 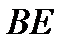 соответственно.
соответственно.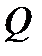 и внутренних изгибающих моментов
и внутренних изгибающих моментов  важно правильно определить их знаки. При этом часто возникают ошибки, так как механически переносят правила знаков, принятые в статике твёрдого тела для внешних силовых факторов.
важно правильно определить их знаки. При этом часто возникают ошибки, так как механически переносят правила знаков, принятые в статике твёрдого тела для внешних силовых факторов. в поперечном сечении балки, которая равна сумме проекций на ось y всех внешних сил, действующих на мысленно отсечённую часть, т.е.
в поперечном сечении балки, которая равна сумме проекций на ось y всех внешних сил, действующих на мысленно отсечённую часть, т.е.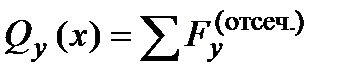 (1)
(1)
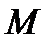 в сечении, который равен сумме моментов внешних сил, действующих на отсечённую часть балки, т.е.
в сечении, который равен сумме моментов внешних сил, действующих на отсечённую часть балки, т.е.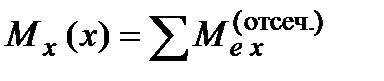 (2)
(2)
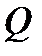 (см. рис.1): для участка
(см. рис.1): для участка  по переменной
по переменной 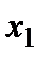 ; для участка
; для участка 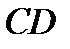 по переменной
по переменной  и для участка DE по переменной
и для участка DE по переменной 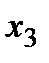 , взятых справа от опоры
, взятых справа от опоры 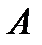 , а для участка
, а для участка 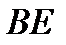 по переменной
по переменной 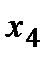 , взятой слева от опоры
, взятой слева от опоры  , т.к. справа от сечения IV-IV внешних сил меньше, чем слева, поэтому вычислить
, т.к. справа от сечения IV-IV внешних сил меньше, чем слева, поэтому вычислить  будет проще:
будет проще: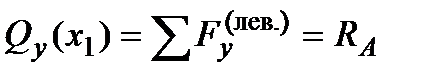 ;
;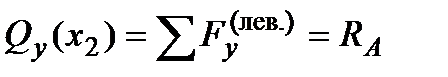 ;
;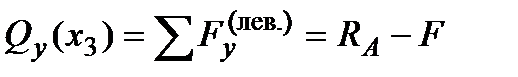 ;
; .
.


