Эпюра 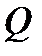 есть график, ординаты которого в каждом сечении выражают в известном масштабе величину внутренней поперечной силы[8].
есть график, ординаты которого в каждом сечении выражают в известном масштабе величину внутренней поперечной силы[8].
Возьмём сечение I-I между точками 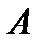 и
и 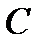 на расстоянии
на расстоянии 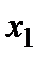 от опоры
от опоры 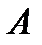 (см. рис.1).
(см. рис.1).
Рассматривая левую отсечённую часть, найдём значение силы  в сечении I-I как сумму внешних сил на этой условно отсечённой левой части балки:
в сечении I-I как сумму внешних сил на этой условно отсечённой левой части балки:
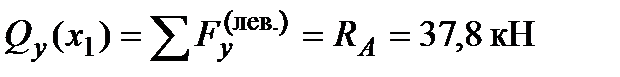 . (3) . (3)
|
Из уравнений (3) видно, что внутренняя поперечная сила на участке 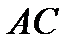 положительна и не зависит от значений абсциссы
положительна и не зависит от значений абсциссы  (переменная
(переменная 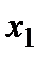 не входит в уравнения (3)), т.е. её эпюра на этом участке балки – линия нулевого порядка (см. Э.Q. рис.1).
не входит в уравнения (3)), т.е. её эпюра на этом участке балки – линия нулевого порядка (см. Э.Q. рис.1).
Для построения эпюры на втором грузовом участке  рассмотрим сечение II-II на расстоянии
рассмотрим сечение II-II на расстоянии 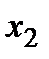 от опоры
от опоры 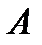 .
.
Выражение (1) для этого участка по переменной 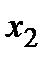 будет аналогично предыдущему, как и по
будет аналогично предыдущему, как и по 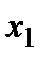 первого участка:
первого участка:
 (4) (4)
|
– (учитываем, что заданный внешний момент 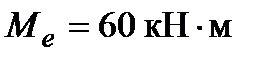 входит только в уравнение моментов).
входит только в уравнение моментов).
Таким образом, на участке 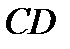 эпюра внутренних поперечных сил будет являться продолжением линии нулевого порядка участка
эпюра внутренних поперечных сил будет являться продолжением линии нулевого порядка участка  с ординатой 37,8 кН.
с ординатой 37,8 кН.
Пользуясь теми же выкладками, составим выражение (1) для сечения III-III между точками 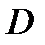 и
и 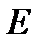 на расстоянии
на расстоянии 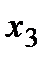 от опоры
от опоры  :
:
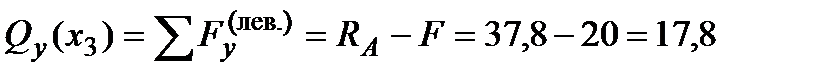 (кН). (5) (кН). (5)
|
Переменная 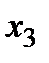 также не входит в уравнение (5), поэтому и на участке
также не входит в уравнение (5), поэтому и на участке 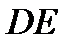 эпюра поперечных сил будет линией нулевого порядка с ординатой 17,8 кН. В точке приложения силы
эпюра поперечных сил будет линией нулевого порядка с ординатой 17,8 кН. В точке приложения силы  кН (Э.Q. рис.1) эпюра поперечных сил делает скачок на величину этой силы.
кН (Э.Q. рис.1) эпюра поперечных сил делает скачок на величину этой силы.
Составим аналитическое выражение (1) для сечения IV-IV между точками В и Е на расстоянии  от правой опоры В:
от правой опоры В:
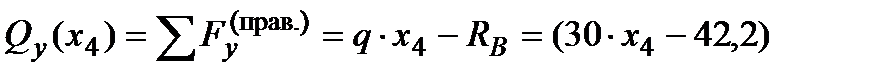 (кН). (6) (кН). (6)
|
Уравнение (6) является уравнением первой степени, т.е. прямой линии (переменная  в первой степени), поэтому её можно построить по двум точкам: достаточно вычислить два крайних значения
в первой степени), поэтому её можно построить по двум точкам: достаточно вычислить два крайних значения 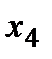 на рассматриваемом участке
на рассматриваемом участке 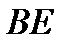 :
:
при 
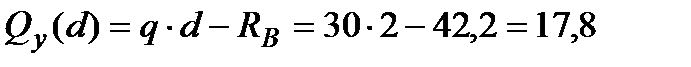 (кН);
(кН);
при 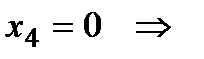
 кН.
кН.
Соединив точки этих двух значений, получаем на участке 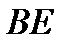 наклонную прямую, которая пересекает нулевую линию (рис.1).
наклонную прямую, которая пересекает нулевую линию (рис.1).
Для построения эпюры внутренних изгибающих моментов[9] 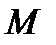 , пользуясь методом сечений, составим аналитическое выражение в общем виде (2) для каждого из четырёх грузовых участков балки по переменным
, пользуясь методом сечений, составим аналитическое выражение в общем виде (2) для каждого из четырёх грузовых участков балки по переменным 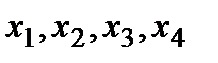 :
:
 (кН×м) (7) (кН×м) (7)
 (кН×м) (8) (кН×м) (8)
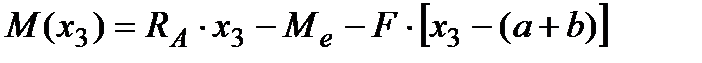 (кН×м) (9) (кН×м) (9)
 (кН×м) (10) (кН×м) (10)
|
Уравнения (7), (8), (9) являются уравнениями первой степени с переменными  , поэтому на участках
, поэтому на участках  ,
,  и
и  момент
момент  будет меняться по закону прямой линии. Для построения эпюры на этих трёх грузовых участках достаточно задаться двумя крайними значениями переменной
будет меняться по закону прямой линии. Для построения эпюры на этих трёх грузовых участках достаточно задаться двумя крайними значениями переменной  для каждого участка, подставить их в формулы (7), (8), (9) и точки найденных значений
для каждого участка, подставить их в формулы (7), (8), (9) и точки найденных значений  соединить прямыми линиями:
соединить прямыми линиями:
при 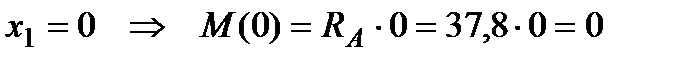 (кН×м);
(кН×м);
при  (кН×м);
(кН×м);
при 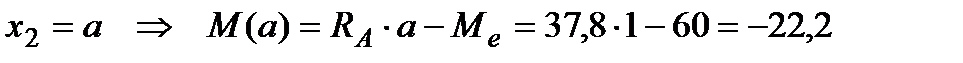 (кН×м);
(кН×м);
при 
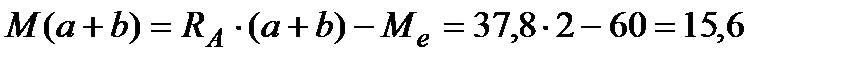 (кН×м);
(кН×м);
при 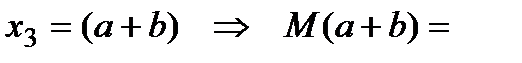
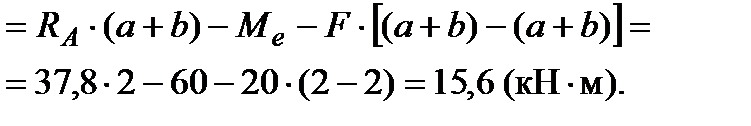
при

Из построения видно (см. Э.Q. рис.1), что в точке приложения внешнего изгибающего момента 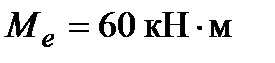 эпюра внутренних изгибающих моментов делает скачок на величину этого момента (претерпевает разрыв).
эпюра внутренних изгибающих моментов делает скачок на величину этого момента (претерпевает разрыв).
В уравнении (10) переменная 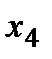 во второй степени, т.е. на участке со сплошной нагрузкой эпюра
во второй степени, т.е. на участке со сплошной нагрузкой эпюра 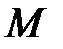 будет представлять собой кривую 2-го порядка – параболу выпуклостью навстречу направлению нагрузки (навстречу «падающему дождю» – правило зонтика).
будет представлять собой кривую 2-го порядка – параболу выпуклостью навстречу направлению нагрузки (навстречу «падающему дождю» – правило зонтика).
Любая парабола эпюры 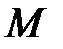 на участке со сплошной нагрузкой строится не менее, чем по трём точкам.
на участке со сплошной нагрузкой строится не менее, чем по трём точкам.
Если на этом участке наклонная прямая эпюры  не пересекает нулевую линию, то все точки параболы
не пересекает нулевую линию, то все точки параболы 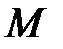 лежат в пределах крайних её значений и парабола не имеет вершины. В этом случае парабола моментов строится при значениях переменной x в двух крайних значениях участка и в середине этого участка.
лежат в пределах крайних её значений и парабола не имеет вершины. В этом случае парабола моментов строится при значениях переменной x в двух крайних значениях участка и в середине этого участка.
Если прямая 1-го порядка эпюры  на участке со сплошной нагрузкой пересекает нулевую линию, (как в нашем примере на участке
на участке со сплошной нагрузкой пересекает нулевую линию, (как в нашем примере на участке  рисунка 1), то парабола эпюры
рисунка 1), то парабола эпюры  на этом участке имеет вершину. Для такого случая третьей точкой параболы будет не середина участка, а вершина параболы.
на этом участке имеет вершину. Для такого случая третьей точкой параболы будет не середина участка, а вершина параболы.
Внутренний изгибающий момент 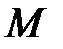 достигает экстремума в тех сечениях, где поперечная сила
достигает экстремума в тех сечениях, где поперечная сила  обращается в нуль. Эти важнейшие следствия вытекают из теоремы Журавского:
обращается в нуль. Эти важнейшие следствия вытекают из теоремы Журавского:
 . (11) . (11)
|
Из этой дифференциальной зависимости вытекает не менее важное следствие: сила 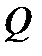 положительна на тех участках балки, где эпюра
положительна на тех участках балки, где эпюра  восходящая линия (при движении слева направо), и отрицательна на тех участках, где эпюра
восходящая линия (при движении слева направо), и отрицательна на тех участках, где эпюра  нисходящая. Следует также обратить внимание на следующие зависимости, вытекающие из формулы (11). На тех участках балки, где изгибающий момент
нисходящая. Следует также обратить внимание на следующие зависимости, вытекающие из формулы (11). На тех участках балки, где изгибающий момент 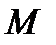 изменяется по параболе (кривая 2-го порядка), поперечная сила
изменяется по параболе (кривая 2-го порядка), поперечная сила  изменяется по линейному закону, т.е. эпюра – наклонная прямая (линия 1-го порядка). Там же, где
изменяется по линейному закону, т.е. эпюра – наклонная прямая (линия 1-го порядка). Там же, где 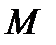 изменяется по линейному закону, т.е. эпюра
изменяется по линейному закону, т.е. эпюра  – наклонная прямая, то поперечная сила
– наклонная прямая, то поперечная сила 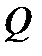 постоянна и её эпюра – горизонтальная прямая (линия нулевого порядка).
постоянна и её эпюра – горизонтальная прямая (линия нулевого порядка).
Вообще порядок функции, описывающей закон изменения 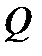 , на единицу ниже порядка функции, выражающей закон изменения
, на единицу ниже порядка функции, выражающей закон изменения 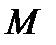 . Это следует непосредственно из формулы (11). Все эти зависимости являются критериями оценки правильности построения эпюр
. Это следует непосредственно из формулы (11). Все эти зависимости являются критериями оценки правильности построения эпюр 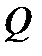 и
и 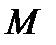 .
.
Вернёмся к нашему примеру. Построим эпюру 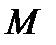 для участка балки
для участка балки 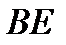 по трём точкам: две точки при крайних значениях переменной
по трём точкам: две точки при крайних значениях переменной  на этом участке (уравнение 10)
на этом участке (уравнение 10)
при  (кН×м);
(кН×м);
при 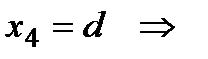
 (кН×м)[10]
(кН×м)[10]
и третьей точки при значении 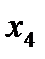 равному расстоянию от опоры
равному расстоянию от опоры  до точки пересечения прямой с нулевой линией на Э.Q. Обозначим это расстояние через
до точки пересечения прямой с нулевой линией на Э.Q. Обозначим это расстояние через  (Э.Q.рис.1).
(Э.Q.рис.1).
Из формулы (11) очевидно, что в этом сечении участка 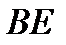 парабола эпюры
парабола эпюры  (рис.1) будет иметь экстремум, т.е. вершину. Найдём координату этого сечения, т.е. определим численное значение
(рис.1) будет иметь экстремум, т.е. вершину. Найдём координату этого сечения, т.е. определим численное значение  .
.
Приравняем уравнение (6) нулю, потому что эпюра 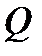 в этой точке пересекает нулевую линию, т.е. значение внутренней поперечной силы
в этой точке пересекает нулевую линию, т.е. значение внутренней поперечной силы 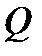 в этом сечении равно нулю:
в этом сечении равно нулю:
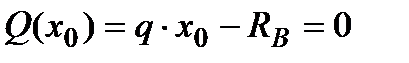 .
.
Отсюда: Þ  (м).
(м).
Значение вершины параболы эпюры  на участке
на участке  (см. формулу 10):
(см. формулу 10):
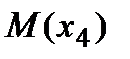 при
при  м
м 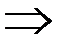
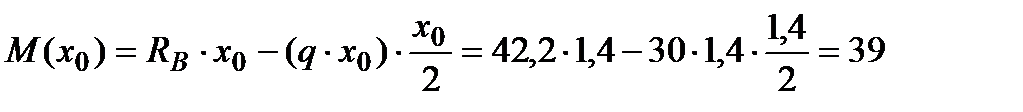 (кН×м).
(кН×м).
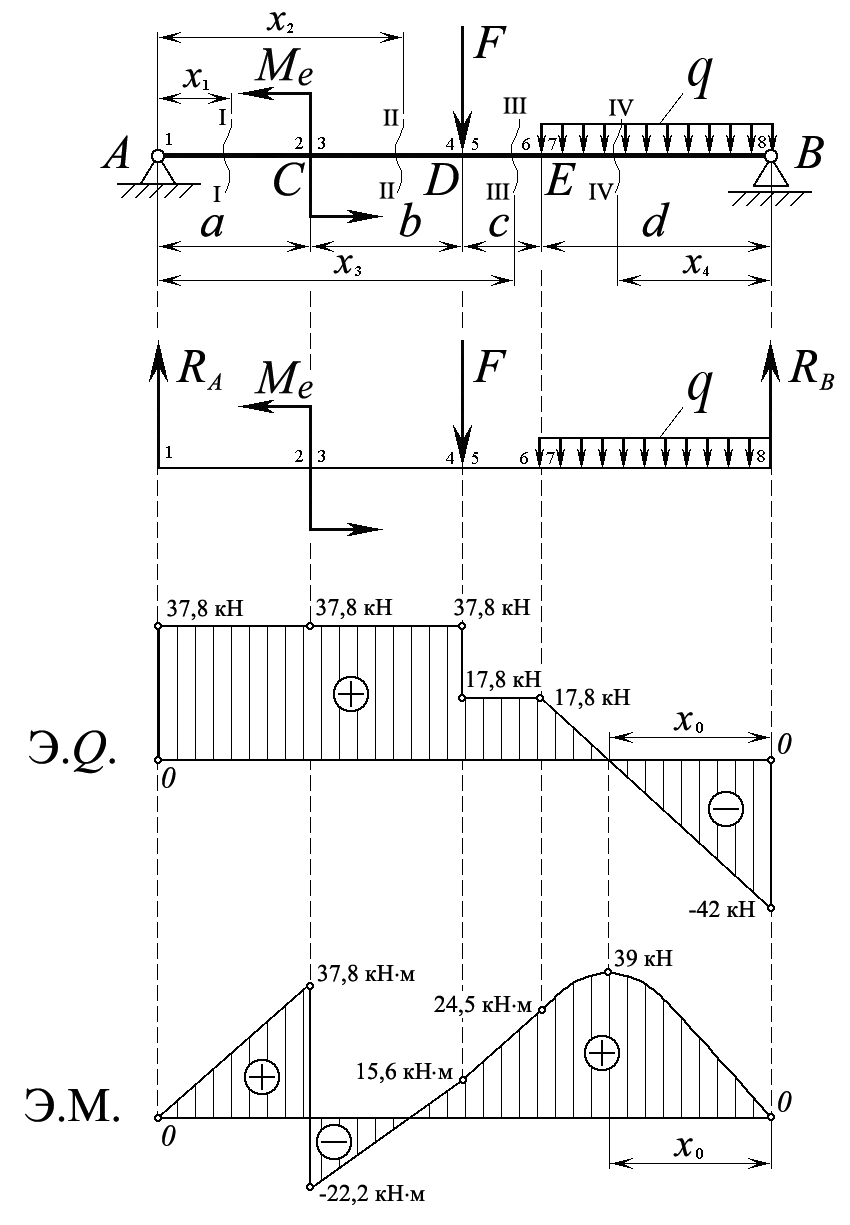
Рис.1.
По трём значениям переменной 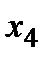 (0; 1,4 м; 2 м) строим параболу на участке
(0; 1,4 м; 2 м) строим параболу на участке 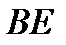 с вершиной
с вершиной  (кН×м) Þ см. рис.1, Э.М. (Для более точного построения параболы М можно рассчитать большее количество точек эпюры, давая значения переменной
(кН×м) Þ см. рис.1, Э.М. (Для более точного построения параболы М можно рассчитать большее количество точек эпюры, давая значения переменной  в пределах рассматриваемого участка).
в пределах рассматриваемого участка).
Площади, ограниченные нулевыми линиями (Э.Q. и Э.М) и построенными линиями эпюр, заштриховываются прямыми линиями, перпендикулярными оси балки (можно цветными карандашами). Площади эпюр 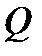 и
и 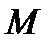 выше нулевых линий обозначают в кружке плюсом Å, а ниже нулевых линий – минусом Θ (см. рис.1).
выше нулевых линий обозначают в кружке плюсом Å, а ниже нулевых линий – минусом Θ (см. рис.1).
Проверяем правильность построения эпюр 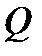 и
и  , пользуясь зависимостями, вытекающими из теоремы Журавского (формула 11).
, пользуясь зависимостями, вытекающими из теоремы Журавского (формула 11).

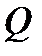 есть график, ординаты которого в каждом сечении выражают в известном масштабе величину внутренней поперечной силы[8].
есть график, ординаты которого в каждом сечении выражают в известном масштабе величину внутренней поперечной силы[8].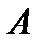 и
и 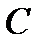 на расстоянии
на расстоянии 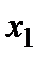 от опоры
от опоры 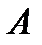 (см. рис.1).
(см. рис.1). в сечении I-I как сумму внешних сил на этой условно отсечённой левой части балки:
в сечении I-I как сумму внешних сил на этой условно отсечённой левой части балки: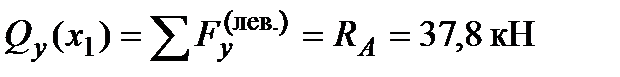 . (3)
. (3)
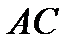 положительна и не зависит от значений абсциссы
положительна и не зависит от значений абсциссы  (переменная
(переменная 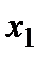 не входит в уравнения (3)), т.е. её эпюра на этом участке балки – линия нулевого порядка (см. Э.Q. рис.1).
не входит в уравнения (3)), т.е. её эпюра на этом участке балки – линия нулевого порядка (см. Э.Q. рис.1). рассмотрим сечение II-II на расстоянии
рассмотрим сечение II-II на расстоянии 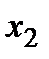 от опоры
от опоры 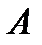 .
.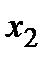 будет аналогично предыдущему, как и по
будет аналогично предыдущему, как и по 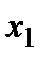 первого участка:
первого участка: (4)
(4)
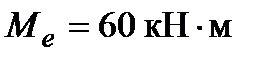 входит только в уравнение моментов).
входит только в уравнение моментов).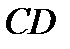 эпюра внутренних поперечных сил будет являться продолжением линии нулевого порядка участка
эпюра внутренних поперечных сил будет являться продолжением линии нулевого порядка участка  с ординатой 37,8 кН.
с ординатой 37,8 кН.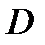 и
и 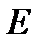 на расстоянии
на расстоянии 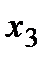 от опоры
от опоры  :
: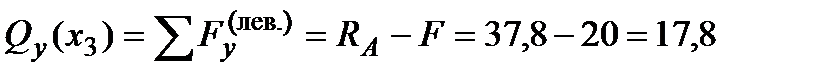 (кН). (5)
(кН). (5)
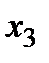 также не входит в уравнение (5), поэтому и на участке
также не входит в уравнение (5), поэтому и на участке 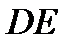 эпюра поперечных сил будет линией нулевого порядка с ординатой 17,8 кН. В точке приложения силы
эпюра поперечных сил будет линией нулевого порядка с ординатой 17,8 кН. В точке приложения силы  кН (Э.Q. рис.1) эпюра поперечных сил делает скачок на величину этой силы.
кН (Э.Q. рис.1) эпюра поперечных сил делает скачок на величину этой силы. от правой опоры В:
от правой опоры В: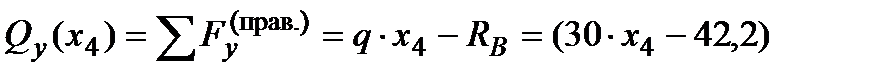 (кН). (6)
(кН). (6)
 в первой степени), поэтому её можно построить по двум точкам: достаточно вычислить два крайних значения
в первой степени), поэтому её можно построить по двум точкам: достаточно вычислить два крайних значения 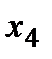 на рассматриваемом участке
на рассматриваемом участке 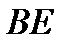 :
:
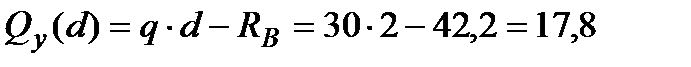 (кН);
(кН);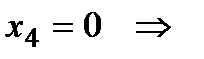
 кН.
кН.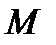 , пользуясь методом сечений, составим аналитическое выражение в общем виде (2) для каждого из четырёх грузовых участков балки по переменным
, пользуясь методом сечений, составим аналитическое выражение в общем виде (2) для каждого из четырёх грузовых участков балки по переменным 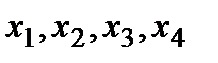 :
: (кН×м) (7)
(кН×м) (7)
 (кН×м) (8)
(кН×м) (8)
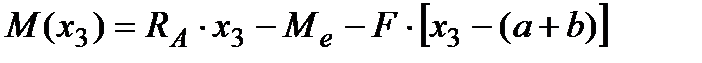 (кН×м) (9)
(кН×м) (9)
 (кН×м) (10)
(кН×м) (10)
 , поэтому на участках
, поэтому на участках  ,
,  и
и  момент
момент  будет меняться по закону прямой линии. Для построения эпюры на этих трёх грузовых участках достаточно задаться двумя крайними значениями переменной
будет меняться по закону прямой линии. Для построения эпюры на этих трёх грузовых участках достаточно задаться двумя крайними значениями переменной  для каждого участка, подставить их в формулы (7), (8), (9) и точки найденных значений
для каждого участка, подставить их в формулы (7), (8), (9) и точки найденных значений  соединить прямыми линиями:
соединить прямыми линиями: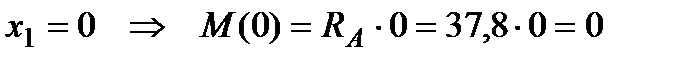 (кН×м);
(кН×м); (кН×м);
(кН×м);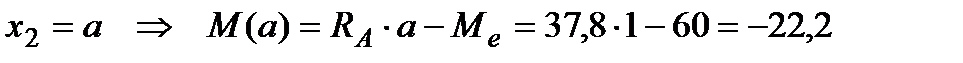 (кН×м);
(кН×м);
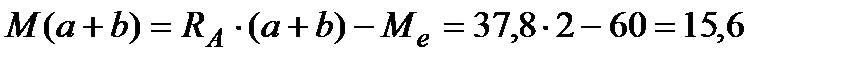 (кН×м);
(кН×м);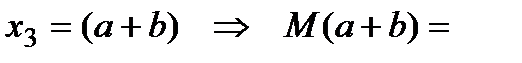
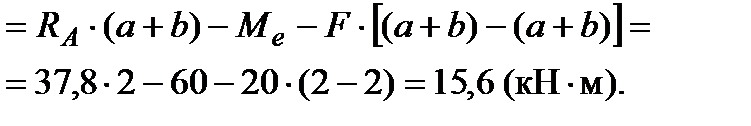

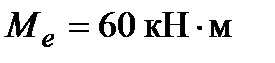 эпюра внутренних изгибающих моментов делает скачок на величину этого момента (претерпевает разрыв).
эпюра внутренних изгибающих моментов делает скачок на величину этого момента (претерпевает разрыв).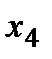 во второй степени, т.е. на участке со сплошной нагрузкой эпюра
во второй степени, т.е. на участке со сплошной нагрузкой эпюра 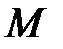 будет представлять собой кривую 2-го порядка – параболу выпуклостью навстречу направлению нагрузки (навстречу «падающему дождю» – правило зонтика).
будет представлять собой кривую 2-го порядка – параболу выпуклостью навстречу направлению нагрузки (навстречу «падающему дождю» – правило зонтика). не пересекает нулевую линию, то все точки параболы
не пересекает нулевую линию, то все точки параболы  на участке со сплошной нагрузкой пересекает нулевую линию, (как в нашем примере на участке
на участке со сплошной нагрузкой пересекает нулевую линию, (как в нашем примере на участке  рисунка 1), то парабола эпюры
рисунка 1), то парабола эпюры  на этом участке имеет вершину. Для такого случая третьей точкой параболы будет не середина участка, а вершина параболы.
на этом участке имеет вершину. Для такого случая третьей точкой параболы будет не середина участка, а вершина параболы. обращается в нуль. Эти важнейшие следствия вытекают из теоремы Журавского:
обращается в нуль. Эти важнейшие следствия вытекают из теоремы Журавского: . (11)
. (11)
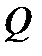 положительна на тех участках балки, где эпюра
положительна на тех участках балки, где эпюра 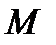 изменяется по параболе (кривая 2-го порядка), поперечная сила
изменяется по параболе (кривая 2-го порядка), поперечная сила  изменяется по линейному закону, т.е. эпюра – наклонная прямая (линия 1-го порядка). Там же, где
изменяется по линейному закону, т.е. эпюра – наклонная прямая (линия 1-го порядка). Там же, где 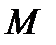 изменяется по линейному закону, т.е. эпюра
изменяется по линейному закону, т.е. эпюра  – наклонная прямая, то поперечная сила
– наклонная прямая, то поперечная сила 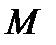 . Это следует непосредственно из формулы (11). Все эти зависимости являются критериями оценки правильности построения эпюр
. Это следует непосредственно из формулы (11). Все эти зависимости являются критериями оценки правильности построения эпюр 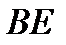 по трём точкам: две точки при крайних значениях переменной
по трём точкам: две точки при крайних значениях переменной  на этом участке (уравнение 10)
на этом участке (уравнение 10) (кН×м);
(кН×м);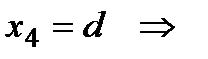
 (кН×м)[10]
(кН×м)[10]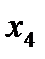 равному расстоянию от опоры
равному расстоянию от опоры  до точки пересечения прямой с нулевой линией на Э.Q. Обозначим это расстояние через
до точки пересечения прямой с нулевой линией на Э.Q. Обозначим это расстояние через  (Э.Q.рис.1).
(Э.Q.рис.1).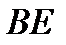 парабола эпюры
парабола эпюры  (рис.1) будет иметь экстремум, т.е. вершину. Найдём координату этого сечения, т.е. определим численное значение
(рис.1) будет иметь экстремум, т.е. вершину. Найдём координату этого сечения, т.е. определим численное значение  .
.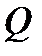 в этой точке пересекает нулевую линию, т.е. значение внутренней поперечной силы
в этой точке пересекает нулевую линию, т.е. значение внутренней поперечной силы 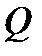 в этом сечении равно нулю:
в этом сечении равно нулю: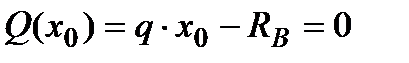 .
. (м).
(м). на участке
на участке 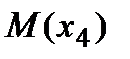 при
при  м
м 
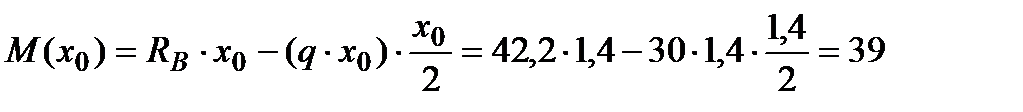 (кН×м).
(кН×м).
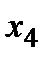 (0; 1,4 м; 2 м) строим параболу на участке
(0; 1,4 м; 2 м) строим параболу на участке 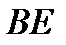 с вершиной
с вершиной  (кН×м) Þ см. рис.1, Э.М. (Для более точного построения параболы М можно рассчитать большее количество точек эпюры, давая значения переменной
(кН×м) Þ см. рис.1, Э.М. (Для более точного построения параболы М можно рассчитать большее количество точек эпюры, давая значения переменной  в пределах рассматриваемого участка).
в пределах рассматриваемого участка). выше нулевых линий обозначают в кружке плюсом Å, а ниже нулевых линий – минусом Θ (см. рис.1).
выше нулевых линий обозначают в кружке плюсом Å, а ниже нулевых линий – минусом Θ (см. рис.1). , пользуясь зависимостями, вытекающими из теоремы Журавского (формула 11).
, пользуясь зависимостями, вытекающими из теоремы Журавского (формула 11).


