| Федеральное агентство
морского и речного транспорта
|
| Федеральное государственное образовательное учреждение
высшего профессионального образования
|
| Государственная морская академия
имени адмирала С.О. Макарова
|
| КАФЕДРА ПРИКЛАДНОЙ МЕХАНИКИ И ИНЖЕНЕРНОЙ ГРАФИКИ
|
| Отчет
о выполнении
расчетно-графической работы
РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ БАЛКИ
|
|
Выполнил:
|
|
|
| Проверил:
|
|
|
|
Санкт-Петербург
2013г.
|
|
Схема нагружения балки № ……. задания А.
Рис.2.
Исходные данные задания А:  ;
;  ;
;  .
.
 ;
;  ;
;  ;
; 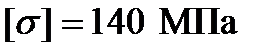 .
.
Профиль:.
ЗАДАЧА I: Построение эпюр Q и М.
а). Определяем значения сил реакций опор 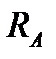 и
и 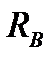 из уравнений статики равновесия моментов и их действительное направление:
из уравнений статики равновесия моментов и их действительное направление:
 ; …………………………………………………………………………………=0;
; …………………………………………………………………………………=0;
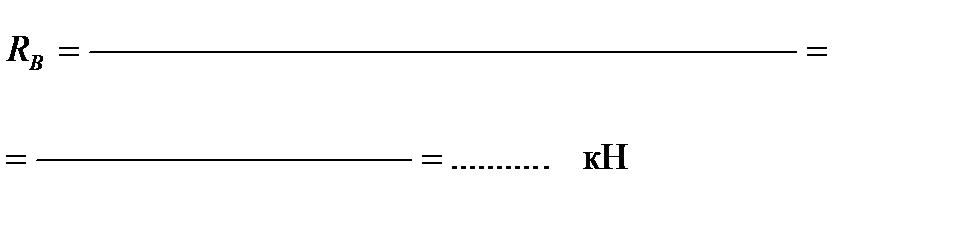
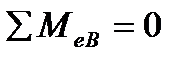 ; ………………………………………………………………………………….=0;
; ………………………………………………………………………………….=0;
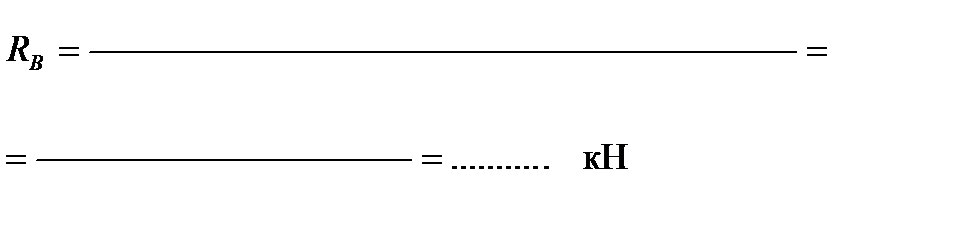
Проверка:
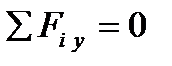 ; …………….………… = ……………………………..=0; Þ 0=0 – тождество!
; …………….………… = ……………………………..=0; Þ 0=0 – тождество!
б). Расчёт 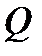 в поперечных сечениях балки и построение графика-эпюры Э.Q.
в поперечных сечениях балки и построение графика-эпюры Э.Q.
* Аналитическое выражение для 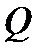 в общем виде для первого участка балки:
в общем виде для первого участка балки:
 (кН).
(кН).
Рассчитываем 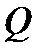 в левом крайнем сечении первого участка (
в левом крайнем сечении первого участка ( ) и правом крайнем (
) и правом крайнем ( ):
):
 (кН);
(кН);
 (кН).
(кН).
* Аналитическое выражение для 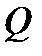 в общем виде для второго участка:
в общем виде для второго участка:
 (кН).
(кН).
Находим 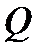 в левом крайнем сечении второго участка (
в левом крайнем сечении второго участка (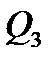 ) и правом крайнем (
) и правом крайнем (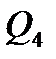 ):
):
 (кН);
(кН);
 (кН).
(кН).
* Аналитическое выражение для 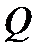 в общем виде для третьего участка:
в общем виде для третьего участка:
 .(кН).
.(кН).
Определяем 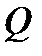 в левом крайнем сечении третьего участка (
в левом крайнем сечении третьего участка ( ) и правом крайнем (
) и правом крайнем (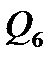 ):
):
 (кН);
(кН);
 (кН).
(кН).
По рассчитанным значениям 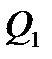 ,
, 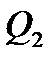 ,
, 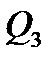 ,
, 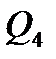 ,
, 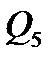 ,
, 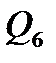 , строим Э.Q. на рис.2.
, строим Э.Q. на рис.2.
в). Расчёт 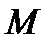 в поперечных сечениях балки и построение графика-эпюры Э.М.
в поперечных сечениях балки и построение графика-эпюры Э.М.
* Аналитическое выражение для 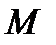 в общем виде для первого участка балки:
в общем виде для первого участка балки:
 (кН×м).
(кН×м).
Рассчитываем 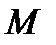 в левом крайнем сечении первого участка (
в левом крайнем сечении первого участка ( ) и правом (
) и правом (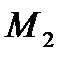 ):
):

 (кН×м);
(кН×м);

 (кН×м);
(кН×м);
* Аналитическое выражение для  в общем виде для второго участка:
в общем виде для второго участка:
 (кН×м).
(кН×м).
Находим  в левом крайнем сечении второго участка (
в левом крайнем сечении второго участка (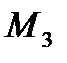 ) и правом (
) и правом (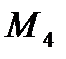 ):
):

 (кН×м);
(кН×м);

 (кН×м);
(кН×м);
* Аналитическое выражение для  в общем виде для третьего участка:
в общем виде для третьего участка:
 (кН×м).
(кН×м).
Определяем 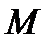 в левом крайнем сечении третьего участка (
в левом крайнем сечении третьего участка ( ) и правом (
) и правом ( ):
):

 (кН×м);
(кН×м);

 (кН×м);
(кН×м);
По рассчитанным значениям  ,
,  ,
, 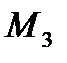 ,
, 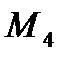 ,
, 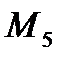 ,
,  строим Э.М. на рис.2.
строим Э.М. на рис.2.
Пользуясь зависимостями, вытекающими из формулы (11), проверяем правильность построения эпюр Q и M.
ЗАДАЧА II: Подбор профиля балки.
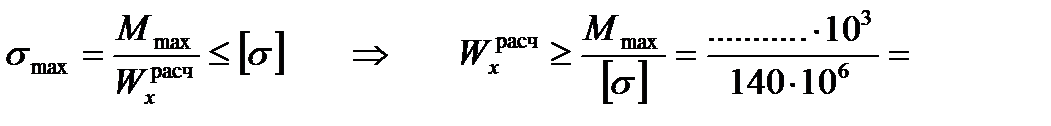
 (м3)
(м3)  (см3).
(см3).
Перегрузка:
Недогрузка:
Из сортамента: 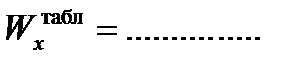 см3 Þ
см3 Þ
Номер профиля № ….………
Схема нагружения балки № ……. задания Б.
Рис.3.
Исходные данные задания Б:  ;
;  ;
;  .
.
 ;
; 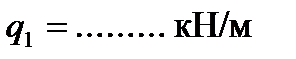 ;
;  ;
; 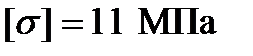 .
.
Профиль:.
ЗАДАЧА I: Построение эпюр Q и М.
а). Определяем значения сил реакций опор 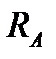 и
и 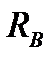 из уравнений статики равновесия моментов и их действительное направление:
из уравнений статики равновесия моментов и их действительное направление:
 ; …………………………………………………………………………………=0;
; …………………………………………………………………………………=0;

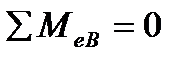 ; ………………………………………………………………………………….=0;
; ………………………………………………………………………………….=0;

Проверка:
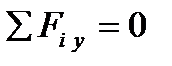 ; …………….………… = ……………………………..=0; Þ 0=0 – тождество!
; …………….………… = ……………………………..=0; Þ 0=0 – тождество!
б). Расчёт 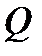 в поперечных сечениях балки и построение графика-эпюры Э.Q.
в поперечных сечениях балки и построение графика-эпюры Э.Q.
* Уравнение для первого участка балки:
 (кН).
(кН).
Рассчитываем Q в левом крайнем сечении первого участка (Q1) и правом – (Q2):
Рассчитываем 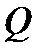 в левом крайнем сечении первого участка (
в левом крайнем сечении первого участка ( ) и правом (
) и правом ( ):
):
 (кН);
(кН);
 (кН).
(кН).
* Уравнение для второго участка:
 (кН).
(кН).
Находим 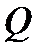 в левом крайнем сечении второго участка (
в левом крайнем сечении второго участка (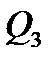 ) и правом (
) и правом (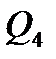 ):
):
 (кН);
(кН);
 (кН).
(кН).
* Уравнение для третьего участка:
 .(кН).
.(кН).
Определяем 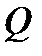 в левом крайнем сечении третьего участка (
в левом крайнем сечении третьего участка ( ) и правом (
) и правом (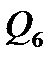 ):
):
 (кН);
(кН);
 (кН).
(кН).
По рассчитанным значениям 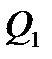 ,
, 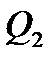 ,
, 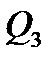 ,
, 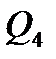 ,
, 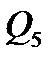 ,
, 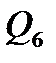 , строим Э.Q. на рис.3.
, строим Э.Q. на рис.3.
в) Расчёт 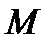 в поперечных сечениях балки и построение графика-эпюры Э.М.
в поперечных сечениях балки и построение графика-эпюры Э.М.
* Уравнение для первого участка балки:
 (кН×м).
(кН×м).
Рассчитываем 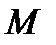 в левом крайнем сечении первого участка (
в левом крайнем сечении первого участка ( ) и правом (
) и правом (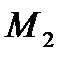 ):
):

 (кН×м);
(кН×м);

 (кН×м);
(кН×м);
* Уравнение для второго участка балки:
 (кН×м).
(кН×м).
Находим  в левом крайнем сечении второго участка (
в левом крайнем сечении второго участка (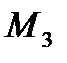 ) и правом (
) и правом (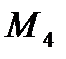 ):
):

 (кН×м);
(кН×м);

 (кН×м);
(кН×м);
* Уравнение для третьего участка балки:
 (кН×м).
(кН×м).
Определяем 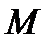 в левом крайнем сечении третьего участка (
в левом крайнем сечении третьего участка ( ) и правом (
) и правом ( ):
):

 (кН×м);
(кН×м);

 (кН×м);
(кН×м);
По рассчитанным значениям  ,
,  ,
, 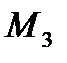 ,
, 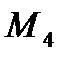 ,
, 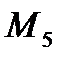 ,
,  строим Э.М. на рис.3.
строим Э.М. на рис.3.
На участках со сплошной нагрузкой парабола эпюры М строится по трём точкам: двум крайним значениям М расчетного участка и в середине участка, если нет вершины параболы. Если имеется вершина параболы, то третья точка – её значение:
……………………………………………………………………………………
……………………………………………………………………………………
……………………………………………………………………………………
……………………………………………………………………………………
……………………………………………………………………………………
Проверяем правильность построения эпюр Q и M на основании теоремы Журавского.
ЗАДАЧА II: Расчёт площади А поперечного сечениябалки.
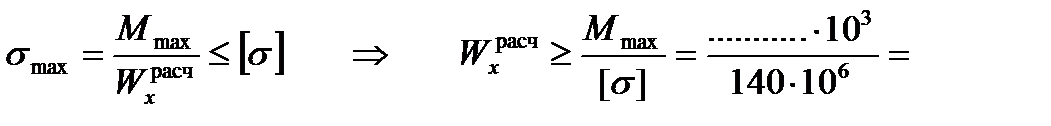
 (м3)
(м3)  (см3).
(см3).
…………………………………………………………………………………….
…………………………………………………………………………………….
 (см2).
(см2).
ВЫВОД
ОГЛАВЛЕНИЕ
| 1. Задание ………………………………………………………..………
|
|
| 2. Состав работы ………………………………..………………………..
|
|
| 3. Порядок выполнения работы ……………………………………..…..
|
|
| 4. Последовательность выполнения работы …………………………..
|
|
| 5. Литература …………………………………………………………….
|
|
| 6. Приложение 1 …………………………………………………………
|
|
| 7. Приложение 2 …………………………………………………………
|
|
| 8. Приложение 3 …………………………………………………………
|
|
| 9. Приложение 4 …………………………………………………………
|
|
| 10. Приложение 5 …………………………………………………………
|
|
| 11. Приложение 6 …………………………………………………………
|
|
| 12. Приложение 7 …………………………………………………………
|
|
| 13. Приложение 8 …………………………………………………………
|
|
| 14. Приложение 9 …………………………………………………………
|
|
| 15. Приложение 10 ………………………………………………………..
|
|
| 16. Оглавление …………………………………………………………….
|
|
[1] Arrangement capacity - схема нагружения (англ.).
[2] Система двух параллельных сил, равных по модулю и направленных в разные стороны, называется парой сил. Расстояние между линиями действия этих сил называется плечом пары. Мерой действия пары сил является алгебраическая величина, называемая её моментом  . Момент пары сил равен по абсолютной величине произведению модуля одной из сил пары на плечо.
. Момент пары сил равен по абсолютной величине произведению модуля одной из сил пары на плечо.
[3] Графически изображать изменение внутренних силовых факторов  и
и 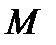 в поперечном сечении балки по её длине в виде эпюр очень удобно. Это придаёт расчёту наглядность, позволяет быстро находить опасные сечения и облегчает подбор размеров сечений балки.
в поперечном сечении балки по её длине в виде эпюр очень удобно. Это придаёт расчёту наглядность, позволяет быстро находить опасные сечения и облегчает подбор размеров сечений балки.
[4] Проверка правильности нахождения сил реакций опор необходима, т.к. в случае ошибки, правильное построение графиков-эпюр  и
и 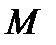 невозможно.
невозможно.
[5] Участок, нагружённый сплошной нагрузкой, при вычислении моментов обычно заменяют равнодействующей с точкой приложения посередине нагружённого участка.
6 Если система находится в равновесии, то сумма изгибающих внешних моментов относительно любого поперечного сечения балки равна нулю.
7 Знак минус значений реакций  или
или 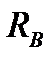 показывает, что принятое вначале направление выбрано неверно и его следует изменить на обратное.
показывает, что принятое вначале направление выбрано неверно и его следует изменить на обратное.
[8] Domestic cross force – внутренняя поперечная сила (англ.).
[9] Domestic bend moment – внутренний изгибающий момент (англ.).
[10] При расчёте изгибающего момента 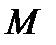 для грузового участка с равномерно распределённой нагрузкой используем теорему Вариньона: момент равнодействующей силы относительно произвольной оси равен сумме моментов сил системы относительно той же оси.
для грузового участка с равномерно распределённой нагрузкой используем теорему Вариньона: момент равнодействующей силы относительно произвольной оси равен сумме моментов сил системы относительно той же оси.
[11] Осевой момент сопротивления (момент сопротивления изгибу) 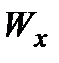 – основная геометрическая характеристика, характеризующая прочность балки.
– основная геометрическая характеристика, характеризующая прочность балки.
[12] Normal stress - нормальное напряжение (англ.).
[13] Индекс adm от admissible (англ.) – допустимый.
[14] Provision durability – условие прочности (англ.).
[15] Axial factor resistance – осевой момент сопротивления (англ.).
[16] Adventurouscross section – опасное поперечное сечение (англ.).
[17] Absolute bend – чистый изгиб (англ.).
[18] height - высота (англ.).

 ;
;  ;
;  .
. ;
;  ;
;  ;
; 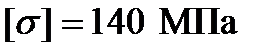 .
.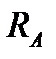 и
и 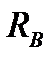 из уравнений статики равновесия моментов и их действительное направление:
из уравнений статики равновесия моментов и их действительное направление: ; …………………………………………………………………………………=0;
; …………………………………………………………………………………=0;
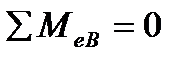 ; ………………………………………………………………………………….=0;
; ………………………………………………………………………………….=0;
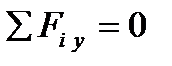 ; …………….………… = ……………………………..=0; Þ 0=0 – тождество!
; …………….………… = ……………………………..=0; Þ 0=0 – тождество!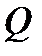 в поперечных сечениях балки и построение графика-эпюры Э.Q.
в поперечных сечениях балки и построение графика-эпюры Э.Q.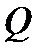 в общем виде для первого участка балки:
в общем виде для первого участка балки: (кН).
(кН).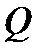 в левом крайнем сечении первого участка (
в левом крайнем сечении первого участка ( ) и правом крайнем (
) и правом крайнем ( ):
): (кН);
(кН); (кН).
(кН).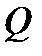 в общем виде для второго участка:
в общем виде для второго участка: (кН).
(кН).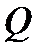 в левом крайнем сечении второго участка (
в левом крайнем сечении второго участка (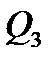 ) и правом крайнем (
) и правом крайнем (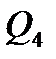 ):
): (кН);
(кН); (кН).
(кН).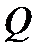 в общем виде для третьего участка:
в общем виде для третьего участка: .(кН).
.(кН).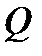 в левом крайнем сечении третьего участка (
в левом крайнем сечении третьего участка ( ) и правом крайнем (
) и правом крайнем (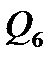 ):
): (кН);
(кН); (кН).
(кН).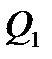 ,
, 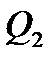 ,
, 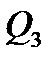 ,
, 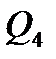 ,
, 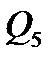 ,
, 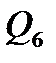 , строим Э.Q. на рис.2.
, строим Э.Q. на рис.2.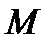 в поперечных сечениях балки и построение графика-эпюры Э.М.
в поперечных сечениях балки и построение графика-эпюры Э.М.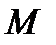 в общем виде для первого участка балки:
в общем виде для первого участка балки: (кН×м).
(кН×м).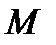 в левом крайнем сечении первого участка (
в левом крайнем сечении первого участка ( ) и правом (
) и правом (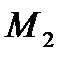 ):
):
 (кН×м);
(кН×м);
 (кН×м);
(кН×м); в общем виде для второго участка:
в общем виде для второго участка: (кН×м).
(кН×м). в левом крайнем сечении второго участка (
в левом крайнем сечении второго участка (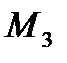 ) и правом (
) и правом (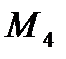 ):
):

 в общем виде для третьего участка:
в общем виде для третьего участка: (кН×м).
(кН×м).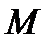 в левом крайнем сечении третьего участка (
в левом крайнем сечении третьего участка ( ) и правом (
) и правом ( ):
):

 ,
,  ,
, 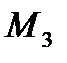 ,
, 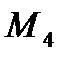 ,
, 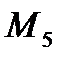 ,
,  строим Э.М. на рис.2.
строим Э.М. на рис.2.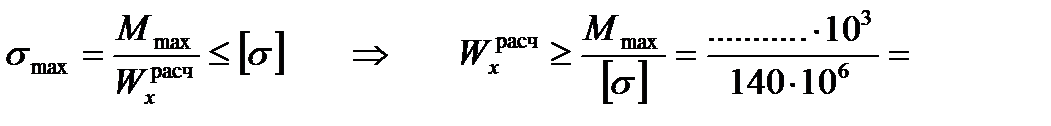
 (м3)
(м3)  (см3).
(см3). см3 Þ
см3 Þ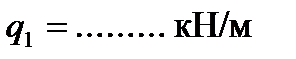 ;
;  ;
; 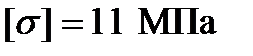 .
.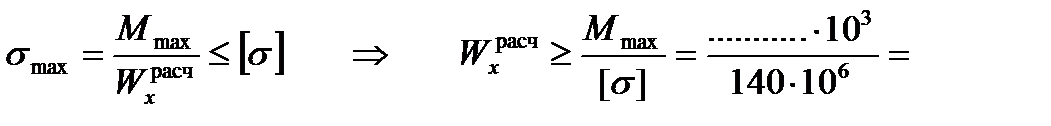
 (см3).
(см3). (см2).
(см2). . Момент пары сил равен по абсолютной величине произведению модуля одной из сил пары на плечо.
. Момент пары сил равен по абсолютной величине произведению модуля одной из сил пары на плечо. и
и 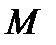 в поперечном сечении балки по её длине в виде эпюр очень удобно. Это придаёт расчёту наглядность, позволяет быстро находить опасные сечения и облегчает подбор размеров сечений балки.
в поперечном сечении балки по её длине в виде эпюр очень удобно. Это придаёт расчёту наглядность, позволяет быстро находить опасные сечения и облегчает подбор размеров сечений балки. или
или 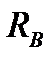 показывает, что принятое вначале направление выбрано неверно и его следует изменить на обратное.
показывает, что принятое вначале направление выбрано неверно и его следует изменить на обратное.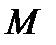 для грузового участка с равномерно распределённой нагрузкой используем теорему Вариньона: момент равнодействующей силы относительно произвольной оси равен сумме моментов сил системы относительно той же оси.
для грузового участка с равномерно распределённой нагрузкой используем теорему Вариньона: момент равнодействующей силы относительно произвольной оси равен сумме моментов сил системы относительно той же оси.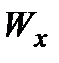 – основная геометрическая характеристика, характеризующая прочность балки.
– основная геометрическая характеристика, характеризующая прочность балки.


