Синусоидальный режим в однородной линии
При периодическом режиме под воздействием приложенного к линии синусоидального напряжения в любой точке линии напряжение и ток изменяются синусоидально с частотой источника. Обозначим комплексные действующие значения напряжения и тока на расстоянии Применяя комплексную форму записи, перепишем уравнения в комплексном виде:
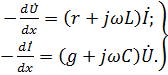
Ввиду того что комплексные значения Исключая из системы (11-4) ток
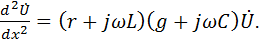
Аналогично, исключая из (11-4) напряжение
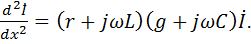
Обозначим квадратный корень из комплексного множителя при
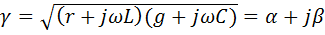
и назовем эту величину коэффициентом распространения. Смысл такого названия выяснится позже. Итак, уравнения (11-5) и (11-6) записываются в виде:

Ток
или
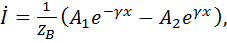
где
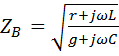
называется волновым сопротивлением линии. Смысл такого названия объяснен дальше. Подставив (11-7) в (11-9), получим:
Мгновенное значение напряжения в точке

здесь Таким образом, мгновенное значение напряжения в любой точке линии слагается из двух функций. Рассмотрим вначале первую из этих слагающих функций. Если считать точку Если же считать момент времени Величина Убывание амплитуды волны вдоль линии обусловливается потерями в линии, а изменение фазы – конечной скоростью распространения электромагнитных колебаний. Оба эти коэффициента На рис. 11-3, а буквой
откуда
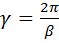 . .
Полученная формула выражает зависимость, существующую между длиной волны и коэффициентом фазы линии. На рис. 11-3, а изображены волны напряжения, соответствующие двум следующим друг за другом моментам времени: С течением времени волна перемещается от начала линии к ее концу; она носит название прямой, или падающей, волны. Скорость перемещения падающей волны вдоль линии, называемая фазовой скоростью волны, определяется как скорость перемещения точки,
Рис. 11-3. Прямая (падающая) (а) и обратная (отраженная) (б) волны.
фаза колебания в которой остается постоянной. Это условие записывается для прямой волны в виде:
откуда
Аналогичное исследование второго слагаемого выражения (11-12) показывает, что для произвольного момента времени оно представляет синусоидальную волну, амплитуда которой Фазовая скорость обратной волны получается равной Итак, мгновенное напряжение можно рассматривать как сумму двух волн, движущихся в противоположных направлениях, причем каждая из этих волн затухает в направлении движения. На основании (11-13) и (11-14)

т. е. за время, равное одному периоду, как падающая, так и отраженная волны перемещаются на расстояние, равное длине волны. Линии, физическая длина которых соизмерима с длиной волны, считаются длинными линиями. При достаточно высоких частотах практически любая протяженная электрическая цепь становится «длинной» по отношению к длине волны. Как будет показано ниже, фазовая скорость в воздушной линии близка к скорости света ( Возвращаясь к уравнениям (11-9) и (11-10) и записывая прямую и обратную волну в комплексной форме, имеем:
где
|

 от начала линии через
от начала линии через  и
и  .
. и
и  не зависят от
не зависят от  и являются только функциями
и являются только функциями 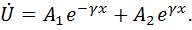


 :
:

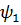 и
и  – аргументы комплексных величин
– аргументы комплексных величин 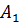 и
и 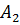 .
.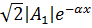 убывает с ростом
убывает с ростом 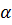 , характеризующая изменение амплитуды волны на единицу длины линии, называется коэффициентом затухания, а величина
, характеризующая изменение амплитуды волны на единицу длины линии, называется коэффициентом затухания, а величина 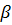 , равная изменению фазы на единицу длины линии, называется коэффициентом фазы.
, равная изменению фазы на единицу длины линии, называется коэффициентом фазы. , который, следовательно, характеризует распространение волны напряжения и тока по линии.
, который, следовательно, характеризует распространение волны напряжения и тока по линии. обозначена длина волны напряжения, равная расстоянию между двумя точками линии, в которых фазы рассматриваемой слагающей напряжения различаются на
обозначена длина волны напряжения, равная расстоянию между двумя точками линии, в которых фазы рассматриваемой слагающей напряжения различаются на  . Следовательно,
. Следовательно,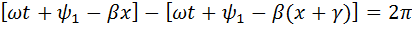 ,
,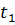 и
и  .
.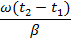
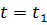


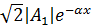
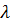


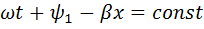 ,
,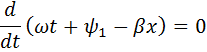
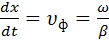 .
.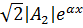 возрастает с увеличение
возрастает с увеличение 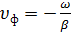 ; знак минус указывает, что обратная волна движется в направлении, противоположном направлению прямой волны.
; знак минус указывает, что обратная волна движется в направлении, противоположном направлению прямой волны. м/сек), и поэтому частоте 50 гц будет соответствовать длина волны 6000 км, а частоте
м/сек), и поэтому частоте 50 гц будет соответствовать длина волны 6000 км, а частоте  гц – длина волны 10 см. Следовательно, в первом случае длинной линией будет линия, измеряемая многими сотнями или тысячами километров, а во втором случае – цепь протяженностью в несколько сантиметров.
гц – длина волны 10 см. Следовательно, в первом случае длинной линией будет линия, измеряемая многими сотнями или тысячами километров, а во втором случае – цепь протяженностью в несколько сантиметров. ,
,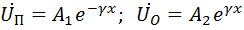 .
.


