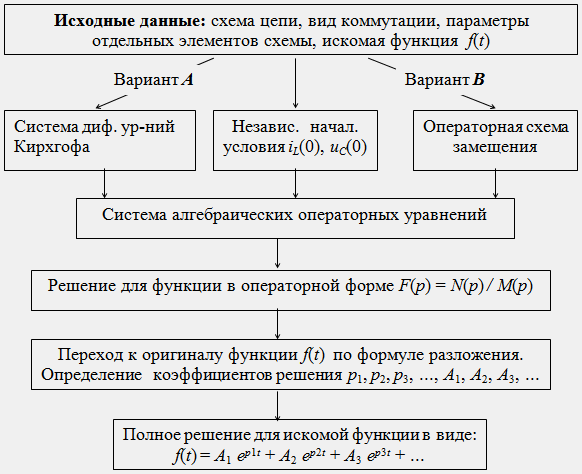
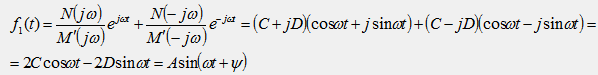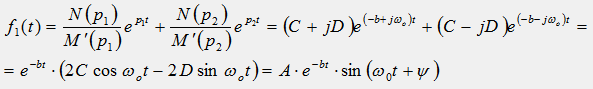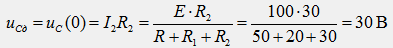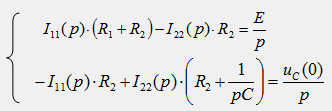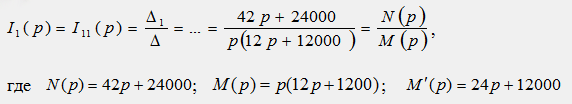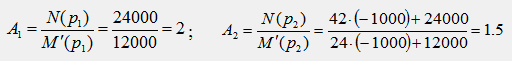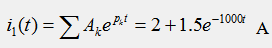Лекции по ТОЭ/ №67 Алгоритм расчета переходных процессов операторным методом.

Замечания к формуле разложения.

1) Если в исходной схеме имеются источники постоянных ЭДС Е, то уравнение M(p)=0 может иметь один корень, равный нулю (p₁=0). Подстановка этого корня в формулу разложения дает постоянную величину f₁(t)=(N(0)/M`(0))e^0*t=const, которая соответствует установившейся составляющей искомой функции.

2) Если в исходной схеме имеются источники синусоидальных ЭДС e(t)=E_msin(ωt+α), то уравнение M(p)=0 будет иметь два чисто мнимых и сопряженных корня p₁=jω и p₂=-jω. Подстановка этих корней в формулу разложения в сумме дает синусоидальную функцию времени,которая соответствует установившейся составляющей искомой функции:

3) Если уравнение имеет два комплексно сопряженных корня p₁=-b+jω и p₂=-b-jω, то подстановка этих корней в формулу разложения в суммe дает синусоидальную функцию с затухающей амплитудой:

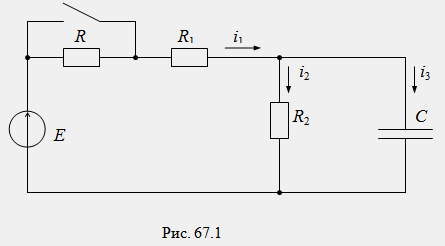
4) Если уравнение имеет кратные корни (p₁=p₂), то формула разложения неприменима. Случай кратных корней может встретиться в практике крайне редко. Чтобы применить формулу разложения в этом случае достаточно несущественно изменить параметры одного из элементов схемы.

Пример. Для схемы рис. 67.1 с заданными параметрами элементов (Е=100 В, R=50 Ом, R1=20 Ом, R2=30 Ом, С=83,5 мкФ) определить ток после коммутации.

 

1) Определяется независимое начальное условие u_C(0)из расчета схемы рис. 67.1 в состоянии до коммутации:

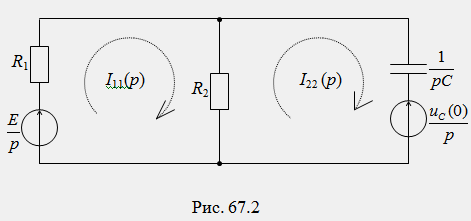
2) Составляется операторная схема цепи после коммутации (рис. 67.2):

3) Составляется система контурных уравнений для схемы рис. 67.2 в операторной форме:

4) Производится решение операторных уравнений относительно искомой функции I₁(p):

6) Коэффициенты A_k для отдельных корней p_k:

7) Окончательное решение для искомой функции времени:

<div><img src="//mc.yandex.ru/watch/9962440" style="position:absolute; left:-9999px;" alt="" /></div>