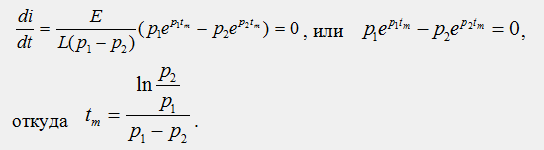А) Корни характеристического уравнения вещественные, не равны друг другу.
Это имеет место при условии:
При изменении t от 0 до ∞ отдельные функции ep1t и ep2t убывают по экспоненциальному закону от 1 до 0, причем вторая из них убывает быстрее, при этом их разность ep1t - ep2t ≥ 0. Из этого следует вывод, что искомая функция тока i(t) в крайних точках при t = 0 и при t = ∞ равна нулю, а в промежутке времени 0 < t < ∞ - всегда положительна, достигая при некотором значении времени tm своего максимального значения Imax. Найдем этот момент времени:
Графическая диаграмма функции i(t) для случая вещественных корней характеристического уравнения показана на рис. 70.2.
Продолжительность переходного процесса в этом случае определяется меньшим по модулю корнем: Tп=4/|pmin|. Характер переходного процесса при вещественных корнях характеристического уравнения получил название затухающего или апериодического.
|