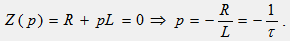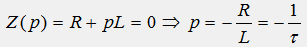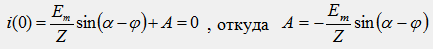Лекции по ТОЭ/ №68 Анализ переходных процессов в цепи R, L.

Исследуем, как изменяется ток i(t) в цепи с резистором R и катушкой L в переходном режиме. В качестве примера рассмотрим переходной процесс при включении цепи R, L к источнику а) постоянной ЭДС e(t)=E=const и б) переменной ЭДС e(t)=Em*sin(ωt+α) (рис. 68.1).

Расчет переходного процесса выполним классическим методом.

а) Включение цепи R, L к источнику постоянной ЭДС e(t)=E=const

Общий вид решения для тока: i(t)=i_y(t)+i_св(t)=I_y+Ae^pt

Установившаяся составляющая тока: I_y=E/R

Характеристическое уравнение и его корни:

Независимое начальное условие: i(0)=0.

Постоянная интегрирования:

Окончательное решение для искомой функции:

где τ=L/R − постоянная времени, численно равная времени, за которое амплитуда свободной составляющей затухает в e=2,72 раза. Чем больше τ, тем медленнее затухает переходной процесс. Теоретически затухание свободной составляющей продолжается до бесконечности. Техническое время переходного процесса T_пп определяется из условия, что за это время свободная составляющая уменьшается до 0,01 от ее первоначального значения:

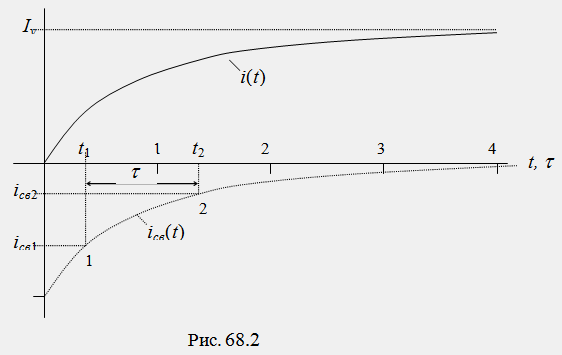
На рис. 68.2 представлена графическая диаграмма искомой функции i(t).

Для приближенного построения графической диаграммы свободной составляющей i_св(t)=Ae^(-t/τ) можно воспользоваться таблицей значений этой функции в интервале времени T_пп=4τ:

Постоянная времени τ может быть определена из графической диаграммы функции i_св(t) как отрезок времени t₂-t₁, по краям которого отношение значений функции равно i_св1/i_св2=e=2,72 раза (рис. 68,2).

б) Включение цепи R, L к источнику синусоидальной ЭДС e(t)=Em*sin(ω+α)

Общий вид решения для тока:

Характеристическое уравнение и его корни:

Установившаяся составляющая тока:

Независимое начальное условие: i(0)=0

Постоянная интегрирования:

Окончательное решение для искомой функции:

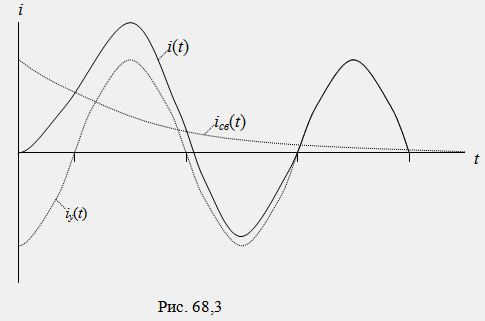
Из анализа решения видно, что амплитуда свободной составляющей А зависит от начальной фазы α источника ЭДС. При α-φ=±α эта амплитуда имеет максимальное значение A=A_max=E_m/Z, при этом переходной процесс протекает с максимальной интенсивностью. При α-φ=0 амплитуда свободной составляющей равна нулю, и переходной процесс в цепи вообще отсутствует. На рис. 68.3 представлена графическая диаграмма искомой функции i(t) при α-φ=-90, A=A_max=E_m/Z=I_m.

<div><img src="//mc.yandex.ru/watch/9962440" style="position:absolute; left:-9999px;" alt="" /></div>