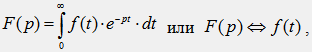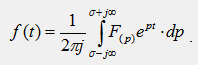Лекции по ТОЭ/ №62 Операторный метод расчета переходных процессов.

Если система дифференциальных уравнений, которыми описывается переходной процесс в схеме, решается операционным методом, то и сам метод расчета переходного процесса также называется операционным или операторным.

Сущность операторного метода состоит в том, что на 1-ом этапе действительные функции времени i(t), u(t), называемые оригиналами, заменяются некоторыми новыми функциями I(p),U(p), называемыми операторными изображениями. Соответствие между оригиналом функции f(t) и ее операторным изображением F(p) устанавливается на основе прямого преобразования интеграла Лапласа:

где ↔ - знак соответствия; p=δ+jω - комплексный оператор Лапласа.

Если δ=0, то p=jω, и преобразование Лапласа превращается в преобразование Фурье, которое лежит в основе комплексного метода расчета цепей переменного тока.

Преобразование Лапласа позволяет заменить операции 2-го рода над оригиналами функций (дифференцирование и интегрирование) на операции 1-го рода (умножение и деление) над операторными изображениями этих функций.

Расчет переходных процессов операторным методом условно выполняется в 3 этапа.

На 1-м этапе расчета система дифференциальных уравнений, составленная по законам Кирхгофа для оригиналов функций, после применения преобразования Лапласа превращается в систему алгебраических уравнений для операторных изображений этих функций.

На 2-ом этапе выполняется решение системы алгебраических операторных уравнений относительно искомой функции, в результате чего получают выражение искомой функции в операторной форме F(p).

На заключительном 3-м этапе выполняется обратный переход от найденного операторного решения для искомой функции F(p) к соответствующей ей функции времени f(t), т. е. Выполняется переход от изображения функции F(p) к ее оригиналу f(t).

Теоретически обратный переход от операторного изображения функции F(p) к ее оригиналу f(t) устанавливается на основе обратного преобразования Лапласа:

На практике для обратного перехода используются более простые и удобные методы, а именно: формула разложения и таблицы соответствия.

<div><img src="//mc.yandex.ru/watch/9962440" style="position:absolute; left:-9999px;" alt="" /></div>