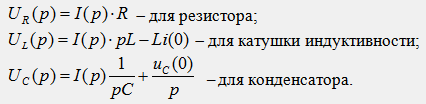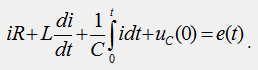Лекции по ТОЭ/ №64 Законы электротехники в операторной форме.

Мгновенные значения тока i(t) и напряжения u(t) на идеальных элементах электрических схем связаны между собой дифференциальной формой уравнений:

Применим к дифференциальным уравнениям преобразование Лапласа и получим соответствующее им операторные изображения:

Таким образом, идеальным элементам R, L, C электрической схемы будут соответствовать новые схемные представления этих элементов в операторной схеме (см. табл.).

Здесь R, pL, 1/pC – операторные сопротивления соответственно резистора R, катушки L и конденсатора C. Операторное сопротивление Z(p) любого участка схемы можно получить из его комплексного сопротивления Z(jω), заменив в выражении множитель jω на оператор p.

Li(0), u_C(0)/p – внутренние источники ЭДС, обусловленные запасами энергии в магнитном и электрическом полях в момент коммутации при t=0. Направления действия внутренних источников ЭДС принимаются по направлению тока i(0) для источника Li(0) и навстречу напряжению u_C(0) для источника u_C(0)/p.

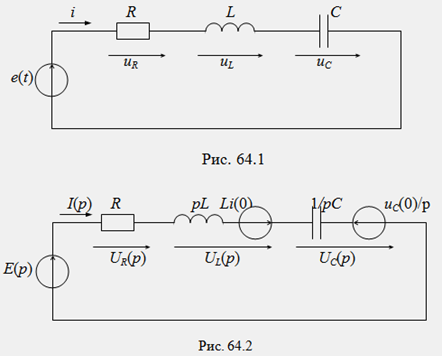
C учетом полученных соотношений любую электрическую схему для оригиналов функций i(t), u(t) можно заменить соответствующей ей операторной схемой для изображений функций I(p),U(p). Например, электрической схеме рис. 64.1 соответствует операторная схема, представленная на рис. 64.2.

Для электрической схемы рис. 64.1 справедливо дифференциальное уравнение, составленное по 2-му закону Кирхгофа:

Для операторной схемы рис. 64.2 справедливо аналогичное уравнение, но в операторной форме:

Для сложных операторных схем справедливы 1-й и 2-й законы Кирхгофа в операторной форме:

Для расчета таких схем можно применять любые методы расчета линейных цепей: метод законов Кирхгофа, метод контурных токов, метод узловых потенциалов и другие. Порядок составления операторных уравнений для сложных схем аналогичен методу, тому порядку, который применяется по этому методу для электрических схем.

<div><img src="//mc.yandex.ru/watch/9962440" style="position:absolute; left:-9999px;" alt="" /></div>