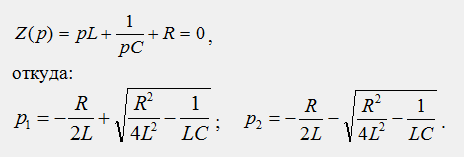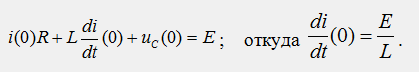Лекции по ТОЭ/ №70 Анализ переходных процессов в цепи R, L, C.
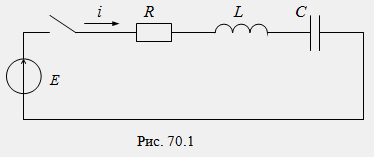
Переходные процессы в цепи R, L, C описываются дифференциальным уравнением 2-го порядка. Установившиеся составляющие токов и напряжений определяются видом источника энергии и определяются известными методами расчета установившихся режимов. Наибольший теоретический интерес представляют свободные составляющие, так как характер свободного процесса оказывается существенно различным в зависимости от того, являются ли корни характеристического уравнения вещественными или комплексными сопряженными. Проанализируем переходной процесс в цепи R, L, C при включении ее к источнику постоянной ЭДС (рис. 70.1).
Общий вид решения для тока: i(t)=iy(t)+iсв(t)=Iy+A1ep2t+A2ep2t Установившаяся составляющая: Iy=0 Характеристическое уравнение и его корни:
Дифференциальное уравнение:
Независимые начальные условия: i(0)=0; uc(0)=0. Зависимое начальное условие:
Постоянные интегрирования определяется из соместного решения системы уравнений:
Окончательное решение для тока:
Исследуем вид функции i(t) при различных значениях корней характеристического уравнения.
|