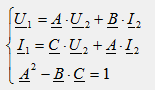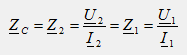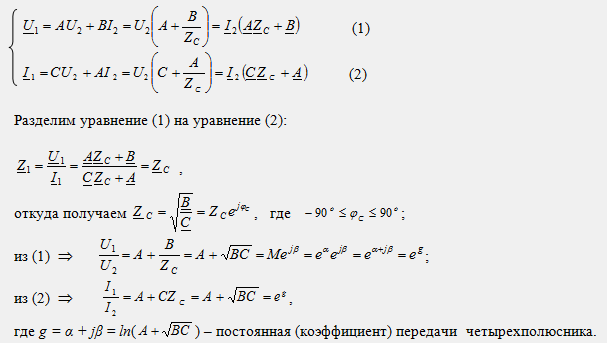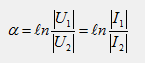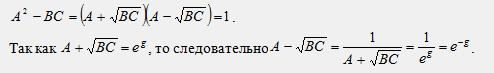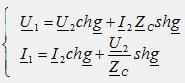Лекции по ТОЭ/ №79 Характеристические параметры симметричного четырехполюсника.
Для симметричного четырехполюсника коэффициент A = D и система уравнений формы А имеет вид:
Характеристическим сопротивлением четырехполюсника Zc называется такое сопротивление нагрузки Z2 = Zc, при котором входное сопротивление четырехполюсника со стороны первичных выводов также равно сопротивлению нагрузки:
Установим связь между характеристическим сопротивлением Zc и коэффициентами четырeхполюсника А, В, С. Для этой цели преобразуем уравнения четырехполюсника:
Вещественная часть коэффициента передачи α показывает, как изменяется модуль напряжения (тока) при переходе через четырехполюсник, поэтому называется коэффициентом затухания:
[Hп] или [Непер] – основная единица измерения затухания. Затухание в 1Нп соответствует уменьшению модуля величины в е = 2,72 раза. На практике для измерения затухания сигналов применяется другая, более удобная для практики единица, а именно: 1 децибелл [дБ], которая определяется согласно уравнению:
Соотношение между единицами затухания: 1Нп = 8,086 дБ; 1дБ = 0,115Нп. Мнимая часть коэффициента передачи показывает, как изменяется фаза напряжения (тока) при переходе через четырехполюсник, поэтому называется коэффициентом фазы:
Характеристическое сопротивление Zc и коэффициент передачи g =α+jβ называются характеристическими параметрами четырехполюсника. Выразим коэффициенты четырехполюсника через его характеристические параметры Zc и g. Преобразуем уравнение связи между коэффициентами:
Решаем совместно полученные уравнения:
С учетом этих выражений основные уравнения формы А получат окончательный вид:
Данная форма уравнений четырехполюсника используется в теории цепных схем и в теории электрических фильтров. <div><img src="//mc.yandex.ru/watch/9962440" style="position:absolute; left:-9999px;" alt="" /></div>
|