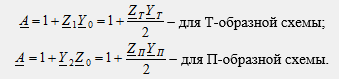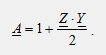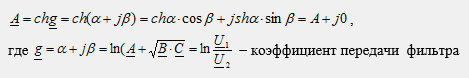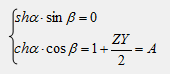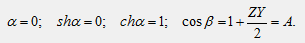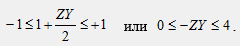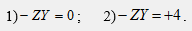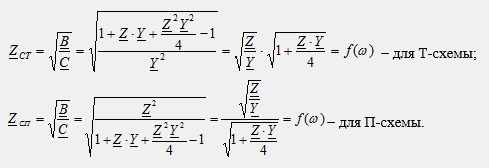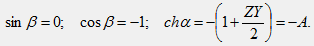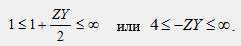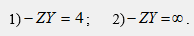Лекции по ТОЭ/ №81 Симметричные реактивные фильтры.
Реактивные фильтры состоят только из реактивных элементов L и C. Существует две простейшие симметричные схемы таких фильтров: Т-образная или Т-схема (рис. 81.1 a) и П-образная или П-схема (рис. 81.1 б).
Рассматривая схемы фильтра как схемы четырехполюсника, выразим коэффициент А через параметры элементов:
Следовательно, независимо от схемы фильтра:
Так как по условию Z и Y являются чисто мнимыми числами, то их произведение Z*Y является чисто вещественным, и, следовательно, коэффициент А также является чисто вещественным. Ранее было получено:
Комплексное уравнение распадается на 2 вещественных:
Полученная система уравнений имеет два решения. 1-е решение:
Это решение соответствует полосе пропускания фильтра и существует при условии ZY<0, что возможно, если одна из этих величин носит индуктивный характер, а другая - емкостный. Диапазон частот, удовлетворяющих решению, определяется соотношением:
Частоты, определяющие границы полосы пропускания фильтра, находятся из решения неравенства:
Характеристическое сопротивление схем может быть выражено через параметры элементов:
В полосе пропускания характеристическое сопротивление фильтра является чисто активным, но зависит от частоты. Это означает, что фильтр не может иметь одинаковый коэффициент передачи для всех частот полосы пропускания, если сопротивление приемника остается постоянным. 2-е решение:
Это решение соответствует полосе задерживания, так как здесь α>0. Границы этой полосы определяются из условия:
Частоты, определяющие границы полосы задерживания фильтра, находятся из решения неравенства:
Характеристическое сопротивление фильтра в полосе задерживания носит реактивный характер и зависит от частоты. <div><img src="//mc.yandex.ru/watch/9962440" style="position:absolute; left:-9999px;" alt="" /></div>
|