Вывод математических моделей, описывающих поведение фотона
Для этого мы должны проследить за волновым движением центра масс На рис. 21 показана схема перемещения центра масс Движение центра масс Движение центра масс Некоторые исследователи отмечали, что фотон имеет скрытые параметры. Если бы удалось найти их, то математические соотношения, описывающие его поведение, вывелись бы аналитически. Попытаемся установить эти параметры.
Рис. 21. Схема движения центра масс М фотона и центра масс
Конечно, сложность модели фотона (рис. 18 и 20) затрудняет вывод математических соотношений, описывающих его поведение. Однако если учесть, что фотон имеет плоскость поляризации, то движение его центра масс
Кинематическим эквивалентом группового движения центров масс шести электромагнитных полей фотона будет вторая условная окружность. Её радиус
Особо отметим, что время, в течение которого эти две условные окружности поворачиваются на разные углы Если угловую скорость условной окружности, описывающей движение центра масс
Из этого имеем:
Соотношение связи между длиной волны
Кинематическая эквивалентность между движением сложной электромагнитной структуры фотона и движением условных окружностей с радиусами Поскольку малая условная окружность радиуса
что соответствует соотношению (62). Аналогичный результат дают и соотношения (77) и (80) второй условной окружности радиуса
Теперь видно, что вывод соотношения (62) не только согласуется с моделью фотона (рис. 17, 18, 20) и механикой её движения (рис. 21), но и объясняет корпускулярные и волновые свойства фотона. При выводе соотношения (56) обратим внимание на то, что кинетическая энергия движения фотона с массой
Тот же самый результат получится и при использовании второй условной окружности радиуса
Приведем уравнение (84) к виду (63)
здесь
С учетом соотношения (79) получаем формулы (67) и (68).
Разделив (87) на (82), имеем
Обратим внимание на то, что Как видно, скрытые параметры позволяют вывести основные математические соотношения Квантовой механики, описывающие поведение фотона, из законов Классической механики. Условные окружности позволяют определить и импульс фотона.
или
Из этого легко получить корпускулярное соотношение Луи Де Бройля
Перепишем это так
В левой части уравнения (93) представлено произведение импульса
Перепишем это неравенство в развернутом виде
Так как фотон проявляет свой импульс в интервале каждой длины волны и так как его размер более двух длин волн (рис. 18, 20, 21), то величины
Обычно неравенство принципа неопределенности записывается в таком виде
или
Полагая, что
Таким образом, модель фотона действительно ограничивает точность экспериментальной информации, получаемой с его помощью. Объясняется это тем, что размеры фотона несколько больше двух длин его волн. Следовательно, фотон не может передать размер геометрической информации, меньший двух длин его волны или двух радиусов вращения, как это и следует из неравенства Гейзенберга. Если мы исследуем объект с помощью фотона с заданной длиной волны, то мы не можем получить геометрическую информацию об объекте, которая была бы равна длине волны используемого фотона или была меньше её. Однако если для получения той же информации использовать фотон с меньшей длиной волны, то точность геометрической информации возрастет. Это значительно ограничивает физический смысл неравенства Гейзенберга. Если это неравенство относить к экспериментальной информации, получаемой с помощью фотона, то оно справедливо только в рамках одной длины его волны или одного радиуса вращения.
|

 всего фотона и центров масс
всего фотона и центров масс  отдельных его электромагнитных полей (рис. 21) [271], [277].
отдельных его электромагнитных полей (рис. 21) [271], [277].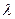 одной волны.
одной волны. от геометрического центра
от геометрического центра  фотона (рис. 21).
фотона (рис. 21). от центра масс
от центра масс 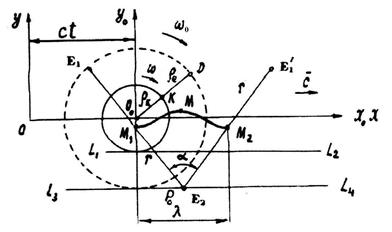
 в интервале длины
в интервале длины 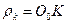 (первый скрытый параметр) условной окружности, описывающей движение этого центра в интервале длины одной волны, определится по формуле (рис. 21)
(первый скрытый параметр) условной окружности, описывающей движение этого центра в интервале длины одной волны, определится по формуле (рис. 21)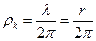 . (76)
. (76)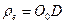 (второй скрытый параметр) определяется из условия поворота центра масс каждого электромагнитного поля
(второй скрытый параметр) определяется из условия поворота центра масс каждого электромагнитного поля 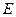 фотона на угол
фотона на угол  в интервале каждой длины
в интервале каждой длины 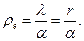 (77)
(77)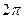 и
и 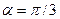 , одно и то же, что соответствует Аксиоме Единства.
, одно и то же, что соответствует Аксиоме Единства. , обозначить через
, обозначить через 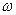 (третий скрытый параметр), а угловую скорость условной окружности, описывающей движение центра масс каждого электромагнитного поля
(третий скрытый параметр), а угловую скорость условной окружности, описывающей движение центра масс каждого электромагнитного поля  (четвертый скрытый параметр), и линейную частоту - через
(четвертый скрытый параметр), и линейную частоту - через 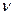 , то период колебаний центра масс фотона определится по формулам (рис. 21):
, то период колебаний центра масс фотона определится по формулам (рис. 21):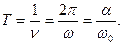 (78)
(78) (79
(79  60)
60)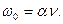 (80)
(80) имеет простой вид (рис. 21)
имеет простой вид (рис. 21) (81
(81 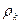 и
и 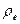 позволяет вывести постулированные раннее математические соотношения, описывающие его поведение (56, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68 и 72, 73, 74, 75). Скрытые, ненаблюдаемые параметры фотона участвуют лишь в промежуточных математических преобразованиях и исчезают в конечных формулах.
позволяет вывести постулированные раннее математические соотношения, описывающие его поведение (56, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68 и 72, 73, 74, 75). Скрытые, ненаблюдаемые параметры фотона участвуют лишь в промежуточных математических преобразованиях и исчезают в конечных формулах. (82
(82  (83
(83 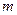 эквивалентна кинетической энергии качения условной окружности с той же массой
эквивалентна кинетической энергии качения условной окружности с той же массой  . (84
. (84 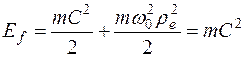 . (85
. (85 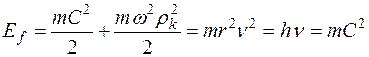 (86
(86 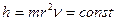 . (87
. (87  ; (88
; (88 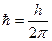 . (89
. (89 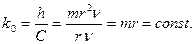

 , формирующей импульсы центра масс
, формирующей импульсы центра масс  , (91
, (91 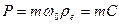 . (91’
. (91’ 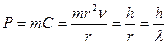 . (92
. (92  . (93)
. (93) фотона на длину его волны
фотона на длину его волны 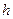 . Из этого следует соотношение неопределенности Гейзенберга.
. Из этого следует соотношение неопределенности Гейзенберга. . (94
. (94  . (95)
. (95)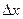 и
и  в неравенстве (95) всегда будут более 2 каждая. Принимая
в неравенстве (95) всегда будут более 2 каждая. Принимая 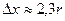 и
и 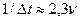 и подставляя эти значения в неравенство (94), получим
и подставляя эти значения в неравенство (94), получим . (96)
. (96) , (97)
, (97)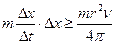 . (98)
. (98)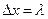 и
и  , получим
, получим или
или 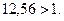 (99)
(99)


