Электромагнитная и магнитная структуры фотона
Поскольку фотон имеет в движении массу Постоянство скорости движения фотонов всех диапазонов указывает на то, что траектории движения центров масс фотонов всех частот - одни и те же. Вполне естественно, что в этом случае и электромагнитная структура фотонов всех частот должна быть одинаковой. Какова эта структура? [270], [277]. Поскольку из равенства Так как фотон имеет массу и электромагнитную природу, то у нас остаётся одна возможность: считать, что массу фотона формируют его электромагнитные поля. Тогда постоянство трех констант Поскольку центробежные силы инерции, действующие на центры масс Из изложенного следует схема электромагнитной модели фотона, показанная на рис. 18.
Рис. 18. Схема электромагнитной модели фотона
Как видно, модель фотона состоит из шести замкнутых друг с другом магнитных полей, которые в соответствии с существующими представлениями о структуре электромагнитного поля при движении модели опоясываются электрическими полями и превращаются в электромагнитные поля. Магнитные поля фотона подобны магнитным полям стержневых магнитов. Векторы напряженности этих магнитных полей чередуются так, что у противоположных полей они направлены вдоль одного диаметра в одну и ту же сторону, сжимая фотон. Но так как фотон все время находится в движении, то магнитные силы, сжимающие фотон, уравновешиваются центробежными силами инерции, действующими на центры масс Если вместо электромагнитных полей образуются кольцевые магнитные поля, подобные кольцевым магнитным полям, которые формируются вокруг проводника с постоянным током (рис. 19), то работоспособность и такой модели фотона сохраняется (рис. 20), и поведение обоих моделей фотона описывается одними и теми же математическими формулами.
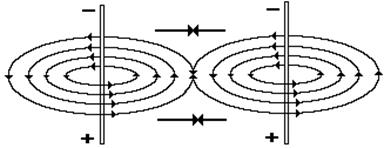
Рис. 19. Схема формирования кольцевых магнитных полей, вокруг провода с постоянным током
Известно, что если силовые линии кольцевых магнитных полей направлены навстречу друг другу, то такие поля сближаются (рис. 19, 20). Если фотон формируют аналогичные кольцевые магнитные поля, то они также будут сближаться (рис. 20), а результирующие силы
Рис. 20. Схема кольцевых магнитных полей фотона
Существует ещё вариант компоновки замкнутых электромагнитных полей, которые обеспечивают сжатие модели при увеличении плотности этих полей. Если в модели (рис. 18) поменять местами электрические и магнитные поля, то её работоспособность сохранится. Сжатие модели будут обеспечивать расположенные вдоль хорд магнитные поля в виде стержневых магнитов и перпендикулярные им кольцевые поля, которые будут направлены навстречу друг другу (рис. 20) в диаметральных направлениях. Таким образом, модель фотона может состоять или из электромагнитных полей или из кольцевых магнитных полей. Мы пока не знаем, какой из этих вариантов реализуется, поэтому в дальнейшем будем писать, что модель фотона формируют электромагнитные поля. Но сразу отмечаем, что магнитная модель (рис. 20) имеет большие шансы на дальнейшее развитие. Сложная, конечно, получается модель, но только в этой модели реализуются все три константы и из анализа её движения выводятся аналитически все математические модели, описывающие поведение фотона в различных экспериментах. Известно, что длина волны электромагнитного излучения изменяется в диапазоне Дальше мы приведём детальное обоснование Конкретную величину температуры в данной точке пространства определяет максимальная совокупность фотонов, длина волны которых определяется по формуле Вина [271], [277]
где Таблица 2. Диапазоны шкалы электромагнитных излучений
Из константы локализации фотона (69) можно извлечь информацию о материальной плотности субстанции (эфира) кольца
или
С увеличением массы (табл. 3), Таблица 3. Диапазоны изменения длины волны
Эта закономерность однозначно следует и из константы локализации фотона Таблица 4. Диапазоны изменения длины волны
C увеличением массы Таким образом, фотоны всех частот, сохраняя свою электромагнитную структуру, меняют массы, частоты и радиусы так, чтобы Такой же четкий и ясный ответ мы получаем и на следующий фундаментальный вопрос: почему фотоны всех частот движутся в вакууме с одинаковой скоростью? Потому, что изменением массы Если наши суждения верны, то из анализа движения полученной модели фотона (рис. 18, 20) мы должны вывести аналитически не только исходные соотношения (56, 58, 59, 60, 62, 62, 63 и 64, 65, 66, 67, 68), описывающие его поведение, но и все остальные, которые используются для интерпретации результатов различных экспериментов с участием фотонов. Вот некоторые из них:
соотношение импульса
неравенство Гейзенберга
уравнение Луи - Де – Бройля, которое описывает волновые свойства фотона
уравнение Э. Шредингера, которое описывает статистику поведения фотонов в некоторых экспериментах
Поскольку в уравнениях (74) и (75) К этим соотношениям добавляются математические модели закона излучения абсолютно черного тела, закона изменения длины волны отраженного фотона в эффекте Комптона, закона формирования спектров атомов и ионов, закона формирования температур, закона локализации температур, закона формирования реликтового излучения, закона фотоэффекта, законов формирования дифракционных и интерференционных картин и др. Все они выводятся из законов классической физики с участием модели фотона, представленной на рис. 18 и 20. Эти выводы будут приведены при анализе каждого из указанных законов. Здесь же мы приведем выводы математических моделей (56, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68 и 72, 73, 74, 75). Обратим внимание ещё раз на то, что в уравнениях Луи Де Бройля (74) и Шредингера (75)
|

 , то вполне естественно, что он имеет и центр масс, то есть такую точку, в которую можно свести всю массу фотона и движение этой точки будет характеризовать движение всего фотона. Волновые свойства фотона указывают на то, что эта точка (центр масс) описывает волновую траекторию.
, то вполне естественно, что он имеет и центр масс, то есть такую точку, в которую можно свести всю массу фотона и движение этой точки будет характеризовать движение всего фотона. Волновые свойства фотона указывают на то, что эта точка (центр масс) описывает волновую траекторию.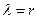 следует, что кольцо разделено хордами на шесть частей (рис. 17, b), то это даёт нам основание предположить, что фотон состоит из шести электромагнитных полей, каждое из которых имеет центр масс
следует, что кольцо разделено хордами на шесть частей (рис. 17, b), то это даёт нам основание предположить, что фотон состоит из шести электромагнитных полей, каждое из которых имеет центр масс 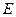 (рис. 17, с).
(рис. 17, с).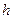 ,
,  и
и  должно обеспечиваться равенством электромагнитных сил, генерируемых движущимися электромагнитными полями, и ньютоновских сил, действующих на центры масс
должно обеспечиваться равенством электромагнитных сил, генерируемых движущимися электромагнитными полями, и ньютоновских сил, действующих на центры масс 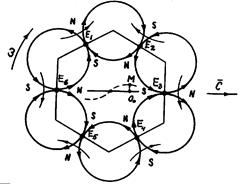
 , возникающие в зонах контакта силовых линий, будут направлены к центру фотона, сжимая его. Но так как он все время находится в движении, то силы
, возникающие в зонах контакта силовых линий, будут направлены к центру фотона, сжимая его. Но так как он все время находится в движении, то силы 
 (табл. 2). Наименьшая длина волны
(табл. 2). Наименьшая длина волны 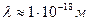 , соответствует гамма диапазону и её можно считать равной радиусу гамма фотона. Наибольшая длина волны
, соответствует гамма диапазону и её можно считать равной радиусу гамма фотона. Наибольшая длина волны 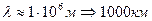 неприемлема для отождествления с радиусом фотона.
неприемлема для отождествления с радиусом фотона. , а здесь лишь отметим, что поскольку тепловую энергию и температуру формируют фотоны, то
, а здесь лишь отметим, что поскольку тепловую энергию и температуру формируют фотоны, то 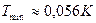 [270], [277].
[270], [277].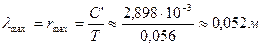 , (70)
, (70) - постоянная Вина - четвёртая константа, контролирующая поведение фотонов. Фотоны с такой длиной волны соответствуют реликтовому диапазону (табл. 2).
- постоянная Вина - четвёртая константа, контролирующая поведение фотонов. Фотоны с такой длиной волны соответствуют реликтовому диапазону (табл. 2).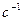


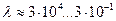
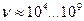
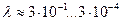
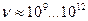
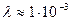
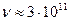
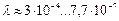

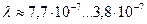
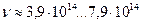


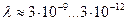
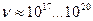
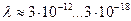
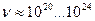
 фотона. Она будет равна:
фотона. Она будет равна: (71)
(71)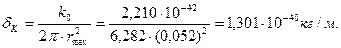 (71 ‘)
(71 ‘) его волны уменьшается.
его волны уменьшается.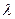 и массы
и массы 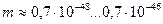


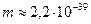
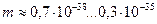
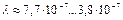
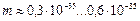



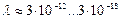

 . Это же следует и из закона сохранения кинетического момента
. Это же следует и из закона сохранения кинетического момента 
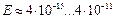
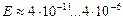

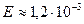
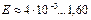


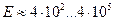

 фотона растет плотность его электромагнитных (рис. 18) или магнитных (рис. 20) полей и за счет этого увеличиваются электромагнитные (магнитные) силы, сжимающие фотон, которые все время уравновешиваются центробежными силами инерции, действующими на центры масс этих полей. Это приводит к уменьшению радиуса
фотона растет плотность его электромагнитных (рис. 18) или магнитных (рис. 20) полей и за счет этого увеличиваются электромагнитные (магнитные) силы, сжимающие фотон, которые все время уравновешиваются центробежными силами инерции, действующими на центры масс этих полей. Это приводит к уменьшению радиуса  фотона, который всегда равен длине его волны
фотона, который всегда равен длине его волны 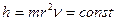 возводится в квадрат, то для сохранения постоянства постоянной Планка частота
возводится в квадрат, то для сохранения постоянства постоянной Планка частота 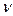 колебаний фотона должна при этом увеличиться. В силу этого незначительное изменение массы
колебаний фотона должна при этом увеличиться. В силу этого незначительное изменение массы 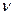 так, что кинетический момент
так, что кинетический момент 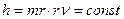 при
при 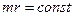 величина
величина 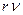 также должна быть постоянной. В результате -
также должна быть постоянной. В результате -  [271], [277].
[271], [277].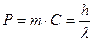 ; (72)
; (72) ; (73)
; (73) ; (74)
; (74) . (75)
. (75) и
и  , где
, где 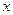 и
и 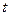 - независимые переменные, то они автоматически работают за рамками аксиомы Единства. Это наглядно проявится при выводе этих уравнений.
- независимые переменные, то они автоматически работают за рамками аксиомы Единства. Это наглядно проявится при выводе этих уравнений.


