Тут уместно обратить внимание на интересную особенность шестигранной механической модели (рис. 17, b). Если взять несколько шестигранников разных размеров и разместить их на наклонной плоскости, то все они будут скатываться вниз с одной и той же постоянной скоростью 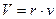 , но с разной частотой (табл. 5).
, но с разной частотой (табл. 5).
Таблица 5. Кинематические параметры движения тел.
| Форма тел
| 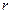 , м , м
| t, с
| V, м/с
| 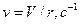
|
| Цилиндрические
| 0,008
0,010
0,0!3
| 2,43
2,30
2,05
| 0,83
0,89
0,99
| -
-
-
|
| Шестигранные
| 0,0065
0,0080
0,0130
| 5,68
5,67
5,67
| 0,18
0,18
0,18
| 27,69
22,50
13,85
|
Обратим внимание на то, что при увеличении радиуса 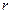 шестигранника частота
шестигранника частота  его движения уменьшается так же, как и у фотона. Конечно, у фотона нет плоскости, по которой он мог бы перемещаться, как тела, представленные в табл. 5. Однако, мы уже показали, что центр масс электромагнитной модели фотона описывает укороченную циклоиду, осью симметрии которой является прямолинейная ось ОХ, лежащая в плоскости его поляризации.
его движения уменьшается так же, как и у фотона. Конечно, у фотона нет плоскости, по которой он мог бы перемещаться, как тела, представленные в табл. 5. Однако, мы уже показали, что центр масс электромагнитной модели фотона описывает укороченную циклоиду, осью симметрии которой является прямолинейная ось ОХ, лежащая в плоскости его поляризации.
Начнем с вывода уравнений движения центра масс  фотона. Поскольку центр масс фотона движется в плоскости поляризации и в рамках аксиомы Единства пространства – материи – времени, то для описания его движения по волновой траектории необходимо иметь два параметрических уравнения [270], [271], [277].
фотона. Поскольку центр масс фотона движется в плоскости поляризации и в рамках аксиомы Единства пространства – материи – времени, то для описания его движения по волновой траектории необходимо иметь два параметрических уравнения [270], [271], [277].
Так как центр масс  фотона движется относительно наблюдателя и относительно геометрического центра
фотона движется относительно наблюдателя и относительно геометрического центра 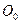 , который движется прямолинейно со скоростью
, который движется прямолинейно со скоростью 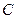 , то для полного описания такого движения необходимо иметь две системы отсчета (рис. 10 и 16): неподвижную
, то для полного описания такого движения необходимо иметь две системы отсчета (рис. 10 и 16): неподвижную 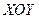 и подвижную
и подвижную 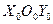 .
.
Амплитуда 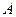 колебаний центра масс
колебаний центра масс  фотона будет равна радиусу
фотона будет равна радиусу 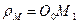 его вращения относительно геометрического центра
его вращения относительно геометрического центра 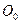 фотона. Из рис. 21 имеем
фотона. Из рис. 21 имеем
 . (100)
. (100)
Обратим внимание на небольшую величину амплитуды 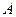 колебаний центра масс фотона в долях длины его волны или радиуса вращения
колебаний центра масс фотона в долях длины его волны или радиуса вращения  .
.
Уравнения движения центра масс  фотона относительно подвижной системы
фотона относительно подвижной системы 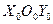 имеют вид параметрических уравнений окружности (рис. 15 и 21):
имеют вид параметрических уравнений окружности (рис. 15 и 21):
 ; (101)
; (101)
 . (102)
. (102)
Если фотон движется относительно неподвижной системы отсчета ХОУ со скоростью 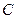 , то уравнения такого движения становятся уравнениями циклоиды:
, то уравнения такого движения становятся уравнениями циклоиды:
 ; (103)
; (103)
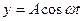 . (104)
. (104)
Обратим внимание на то, что в уравнениях (103) и (104) 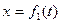 и
и 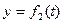 . Это значит, что они описывают движение центра масс фотона по волновой траектории в рамках аксиомы Единства пространства – материи – времени. Отметим, что уравнения Луи Де Бройля (74) и Шредингера (75) этим свойством не обладают. Учитывая соотношения (79), (80) и (100), получим:
. Это значит, что они описывают движение центра масс фотона по волновой траектории в рамках аксиомы Единства пространства – материи – времени. Отметим, что уравнения Луи Де Бройля (74) и Шредингера (75) этим свойством не обладают. Учитывая соотношения (79), (80) и (100), получим:
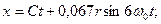 (105)
(105)
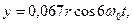 (106)
(106)
где 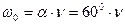 .
.
На рис. 22 представлены траектории точек  , показанные на (рис. 15). Обратим внимание на важные особенности. Радиус кольца равен
, показанные на (рис. 15). Обратим внимание на важные особенности. Радиус кольца равен 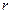 и точка
и точка  , лежащая на кольце (рис. 15), описывает обыкновенную циклоиду М (рис. 22) [8], [26].
, лежащая на кольце (рис. 15), описывает обыкновенную циклоиду М (рис. 22) [8], [26].
Радиус окружности, описываемой точкой  (рис. 15 и 22), -
(рис. 15 и 22), -  и эта точка описывает удлинённую циклоиду
и эта точка описывает удлинённую циклоиду  (рис. 22).
(рис. 22).

Рис. 22. Траектории движения точек  , представленных на рис. 15:
, представленных на рис. 15:
М – обыкновенная циклоида; N – удлинённая циклоида; К – укороченная циклоида;
Радиус окружности, описываемой точкой 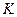 (рис. 15 и 22),
(рис. 15 и 22), 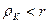 , и она описывает укороченную циклоиду
, и она описывает укороченную циклоиду 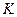 (рис. 17).
(рис. 17).
Так как у модели фотона амплитуда 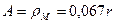 , то его центр масс движется по укороченной циклоиде (105), (106).
, то его центр масс движется по укороченной циклоиде (105), (106).
Результаты табл. 5 требуют, чтобы математическая модель, описывающая скорость центра масс шестигранника, а значит и фотона, не зависела бы от его радиуса 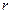 вращения. Уравнения (105) и (106) автоматически дают такой результат
вращения. Уравнения (105) и (106) автоматически дают такой результат
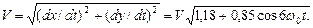
Если считать, что движение фотона эквивалентно движению шестигранника, то  и получаем закономерность изменения скорости центра масс фотона, в которую легко вводятся электрическая
и получаем закономерность изменения скорости центра масс фотона, в которую легко вводятся электрическая 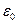 и магнитная
и магнитная  постоянные
постоянные 
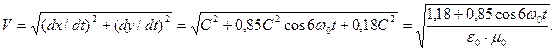 (107)
(107)
График скорости (107) центра масс фотона показан на рис. 23, а.
Как видно, скорость центра масс  фотона действительно изменяется в интервале длины волны или периода колебаний таким образом, что её средняя величина остается постоянной и равной
фотона действительно изменяется в интервале длины волны или периода колебаний таким образом, что её средняя величина остается постоянной и равной 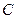 [270], [271], [277].
[270], [271], [277].
Поскольку сила инерции направлена противоположно ускорению, то касательная составляющая силы инерции  , действующая на центр масс фотона, запишется так
, действующая на центр масс фотона, запишется так
 . (108)
. (108)
Несмотря на сложность переменной составляющей математической модели (108), касательная сила инерции, действующая на центр масс фотона, изменяется синусоидально (рис 23, b). Это значит, что она генерирует прямолинейное движение фотона так же, как и сила инерции, движущая автомобиль (рис. 3, b) или силы инерции дисбалансов, вращающие потребителя механической энергии электромотора, о которых мы подробно расскажем в ответах на вопросы.
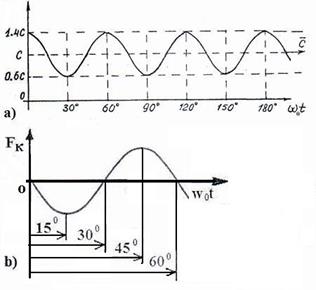
Рис. 23. а) - график скорости центра масс фотона; b) - зависимость изменения силы

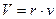 , но с разной частотой (табл. 5).
, но с разной частотой (табл. 5).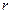 , м
, м
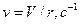
 его движения уменьшается так же, как и у фотона. Конечно, у фотона нет плоскости, по которой он мог бы перемещаться, как тела, представленные в табл. 5. Однако, мы уже показали, что центр масс электромагнитной модели фотона описывает укороченную циклоиду, осью симметрии которой является прямолинейная ось ОХ, лежащая в плоскости его поляризации.
его движения уменьшается так же, как и у фотона. Конечно, у фотона нет плоскости, по которой он мог бы перемещаться, как тела, представленные в табл. 5. Однако, мы уже показали, что центр масс электромагнитной модели фотона описывает укороченную циклоиду, осью симметрии которой является прямолинейная ось ОХ, лежащая в плоскости его поляризации. фотона. Поскольку центр масс фотона движется в плоскости поляризации и в рамках аксиомы Единства пространства – материи – времени, то для описания его движения по волновой траектории необходимо иметь два параметрических уравнения [270], [271], [277].
фотона. Поскольку центр масс фотона движется в плоскости поляризации и в рамках аксиомы Единства пространства – материи – времени, то для описания его движения по волновой траектории необходимо иметь два параметрических уравнения [270], [271], [277].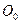 , который движется прямолинейно со скоростью
, который движется прямолинейно со скоростью 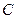 , то для полного описания такого движения необходимо иметь две системы отсчета (рис. 10 и 16): неподвижную
, то для полного описания такого движения необходимо иметь две системы отсчета (рис. 10 и 16): неподвижную 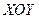 и подвижную
и подвижную 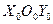 .
.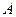 колебаний центра масс
колебаний центра масс 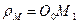 его вращения относительно геометрического центра
его вращения относительно геометрического центра  . (100)
. (100) .
. ; (101)
; (101) . (102)
. (102) ; (103)
; (103)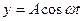 . (104)
. (104)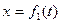 и
и 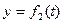 . Это значит, что они описывают движение центра масс фотона по волновой траектории в рамках аксиомы Единства пространства – материи – времени. Отметим, что уравнения Луи Де Бройля (74) и Шредингера (75) этим свойством не обладают. Учитывая соотношения (79), (80) и (100), получим:
. Это значит, что они описывают движение центра масс фотона по волновой траектории в рамках аксиомы Единства пространства – материи – времени. Отметим, что уравнения Луи Де Бройля (74) и Шредингера (75) этим свойством не обладают. Учитывая соотношения (79), (80) и (100), получим: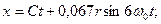 (105)
(105)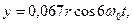 (106)
(106)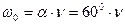 .
. , показанные на (рис. 15). Обратим внимание на важные особенности. Радиус кольца равен
, показанные на (рис. 15). Обратим внимание на важные особенности. Радиус кольца равен  (рис. 15 и 22), -
(рис. 15 и 22), -  и эта точка описывает удлинённую циклоиду
и эта точка описывает удлинённую циклоиду 
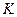 (рис. 15 и 22),
(рис. 15 и 22), 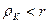 , и она описывает укороченную циклоиду
, и она описывает укороченную циклоиду 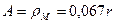 , то его центр масс движется по укороченной циклоиде (105), (106).
, то его центр масс движется по укороченной циклоиде (105), (106).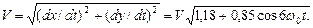
 и получаем закономерность изменения скорости центра масс фотона, в которую легко вводятся электрическая
и получаем закономерность изменения скорости центра масс фотона, в которую легко вводятся электрическая 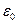 и магнитная
и магнитная  постоянные
постоянные 
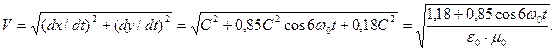 (107)
(107) , действующая на центр масс фотона, запишется так
, действующая на центр масс фотона, запишется так . (108)
. (108)



