Отражение и поляризация фотонов
Поскольку фотон вращается относительно своей оси и движется поступательно, то такое движение называется плоскопараллельным, а плоскость вращения – плоскостью поляризации. Спин фотона равен постоянной Планка
Рис. 24. Упрощенные схемы моделей фотонов: а) с правоциркулярной и b) левоциркулярной поляризациями
Обратим внимание на главное: направление вектора Мы уже показали, что движение центра масс такой модели описывают уравнения (103) и (104), а изменение скорости центра масс фотона описывается уравнением (107). Для анализа процесса отражения фотона необходимо знать закономерность изменения направления вектора импульса центра масс фотона. Угол между направлением вектора импульса
где Центр масс фотона находится на гребне волны при Отсутствие поперечной составляющей импульса у всех отражающихся фотонов должно приводить их к поляризации в момент отражения. Вполне естественно, что в неполяризованном луче плоскости вращения фотонов будут параллельны направлению движения луча света и ориентированы произвольно (рис. 25, падающий луч 1). В дальнейшем мы будем характеризовать поляризацию фотонов плоскостями их вращения. Поляризация отраженных фотонов была открыта Этьен Малюсом в 1808 г [221]. Возникает вопрос: все ли фотоны поляризуются после отражения так, что плоскость их поляризации совпадает с плоскостью падения 3 и плоскостью отражения 4? Ответ на этот вопрос дал Френель (рис. 25) [221].
Рис. 25. Схема поляризации отраженных фотонов: 1 – падающий луч; 2 – отраженный луч; 3 – плоскость падения; 4 – плоскость отражения; 5 – отражающая плоскость; 6 – вертикальная жирная линия символизирует количество фотонов, поляризованных в вертикальной плоскости (плоскости отражения (4)
Он установил, что фотоны, поляризованные в плоскости падения 3 и перпендикулярно ей, после отражения не меняют направление своих плоскостей поляризации. Если же плоскости поляризации фотонов не параллельны и не перпендикулярны плоскости падения 3, то отражение таких фотонов сопровождается поворотом плоскостей их поляризации в таком направлении, что все они оказываются поляризованными в плоскости отражения 4, совпадающей с плоскостью падения 3. Из этого следует, что в падающем луче света направление своей плоскости поляризации после отражения изменяют лишь те фотоны, у которых угол Широкая вертикальная полоса 6 в отраженном луче 2 символизирует поляризацию большей части фотонов, совпадающую с плоскостью его отражения 4. Узкая горизонтальная линия символизирует сохранение поляризации фотонов в плоскости, перпендикулярной плоскости падения 3 и плоскости отражения 4. Таким образом, если плоскость поляризации падающего фотона (рис. 25) перпендикулярна плоскости падения 3 или лежит в ней, то плоскость 5, на которую падает фотон, не меняет направление плоскости его поляризации. Если же плоскость поляризации падающего фотона не перпендикулярна плоскости падения 3, то отражающая плоскость 5 изменяет её направление так, что она становится параллельной плоскости отражения 4. Таким образом, в отраженном луче большая часть фотонов поляризована в плоскости отражения 4 и меньшая часть в плоскости, перпендикулярной плоскости отражения. Возникает вопрос: почему фотоны ведут себя так? Ответ на него мы опубликовали в 1990 г [8], [26]. Если плоскость поляризации фотона не перпендикулярна плоскости падения 3, то все фотоны начинают контактировать с отражающей плоскостью 5 одним (из шести) электромагнитным (магнитным) полем, что облегчает процесс поворота их плоскостей поляризации. При этом, если угол падения равен или близок к Когда плоскость поляризации фотона перпендикулярна плоскости падения 3, то фотон, сближаясь с отражающей плоскостью 5, контактирует с ней в основном двумя электромагнитными (магнитными) полями, что увеличивает устойчивость процесса контакта и затрудняет поворот плоскости поляризации фотона. Теперь нам необходимо запомнить ориентиры поляризации фотонов. Первый и главный – плоскость вращения фотона совпадает с плоскостью поляризации и направлением движения фотонов. Второй - направление спина Через сосуд 5 с водой, взмученной каплей молока, проходит свет. Если он идет от источника 9, не отражаясь от экрана (рис. 26, а), то в индикаторе поляризации, роль которого выполняет сосуд 5, и на экране 4 наблюдается рассеяние света во всех направлениях (9, 10). Если же через этот же сосуд проходит луч света (рис 26, b) отраженный под углом примерно
Рис. 26. Поляризация света при отражении: 1-падающий луч; 2 – отражающая плоскость; 3 – отраженный луч; 4 – экран; 5 – сосуд с взмученной водой; 6 – луч, прошедший через сосуд; 7 – плоскость падения луча; 8 – плоскость поляризации отраженного луча; 9 – неполяризованный луч источника света; 10 – неполяризованный луч, прошедший через сосуд 5
Таким образом, луч света, проходящий через сосуд без предварительного отражения, рассеивается во всех направлениях, что указывает на то, что фотоны в нём сохраняют исходную поляризацию 9, 10. Если же в сосуд направить такой же, но отраженный луч, то он, отражаясь, поляризуется и, проходя через сосуд, рассеивается в основном в горизонтальной плоскости 7. Это является доказательством того, что отраженный луч поляризован в основном в плоскости падения 7 (рис. 26, b), как это показано на экране 4. Простой опыт, проведённый С. И. Вавиловым, является косвенным доказательством отсутствия поперечной составляющей импульса у отраженных фотонов (139) [228]. Из этого также следует, что независимо от направления плоскостей поляризации падающих фотонов плоскость поляризации отраженных фотонов 3 совпадает с плоскостью падения 7. Далее, необходимо знать детали процесса отражения поляризованных фотонов. На рис. 27 показаны зависимости коэффициента отражения фотонов с разной поляризацией на границе воздух-стекло. Обратим внимание на то, что при совпадении плоскостей падения, отражения и поляризации фотонов коэффициент отражения при угле падения, близком к
Рис. 27. Зависимость коэффициента отражения фотонов от границы воздух – стекло от угла падения 1 – плоскости падения фотонов и поляризации перпендикулярны; 2 – неполяризованный луч; 3 – плоскости падения, поляризации и отражения фотонов совпадают
Мы уже описали причину такого поведения фотонов. При угле падения, близком к
|

 и направлен вдоль оси его вращения перпендикулярно направлению его движения (рис. 17, а, b, c). Тогда упрощенная модель правоциркулярного фотона будет такой, как показано на рис. 24, а, левоциркулярного – на рис. 24, b.
и направлен вдоль оси его вращения перпендикулярно направлению его движения (рис. 17, а, b, c). Тогда упрощенная модель правоциркулярного фотона будет такой, как показано на рис. 24, а, левоциркулярного – на рис. 24, b.
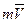 центра масс фотона и осью ОХ определяется по формуле
центра масс фотона и осью ОХ определяется по формуле , (139)
, (139)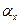 - угол наклона результирующего вектора импульса
- угол наклона результирующего вектора импульса 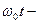 угол поворота центра масс одного электромагнитного (магнитного) поля фотона относительно центра масс фотона;
угол поворота центра масс одного электромагнитного (магнитного) поля фотона относительно центра масс фотона;  - угол, определяющий количество электромагнитных (магнитных) полей фотона, замкнутых друг с другом по круговому контуру.
- угол, определяющий количество электромагнитных (магнитных) полей фотона, замкнутых друг с другом по круговому контуру. и
и  , и - в яме волны при
, и - в яме волны при 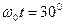 и
и 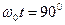 . Поскольку модель фотона электромагнитная, то он легко деформируется при встрече с препятствием. При этом в момент отражения центр масс фотона находится преимущественно на гребне или в яме волны, то есть при
. Поскольку модель фотона электромагнитная, то он легко деформируется при встрече с препятствием. При этом в момент отражения центр масс фотона находится преимущественно на гребне или в яме волны, то есть при 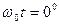 и
и  . То есть в момент отражения фотона отсутствует поперечная составляющая импульса
. То есть в момент отражения фотона отсутствует поперечная составляющая импульса 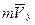 . Это значит, что плоскость падения 3 луча 1, состоящего из фотонов, и плоскость его отражения 4 должны совпадать независимо от ориентации плоскостей поляризации фотонов (рис. 24, 25).
. Это значит, что плоскость падения 3 луча 1, состоящего из фотонов, и плоскость его отражения 4 должны совпадать независимо от ориентации плоскостей поляризации фотонов (рис. 24, 25).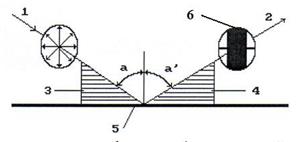
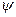 между плоскостью падения 3 луча 1 и плоскостью поляризации находится в интервале
между плоскостью падения 3 луча 1 и плоскостью поляризации находится в интервале 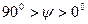 . Те же фотоны, у которых плоскость поляризации перпендикулярна (
. Те же фотоны, у которых плоскость поляризации перпендикулярна ( ) плоскости падения 3 или совпадает с ней (
) плоскости падения 3 или совпадает с ней (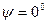 ), отражаются, не меняя ориентации своей плоскости поляризации. Фактически, отраженные фотоны поляризуются в двух взаимно перпендикулярных плоскостях, одна из которых совпадает с плоскостью падения 3, а другая - перпендикулярна ей. Из описания Френеля следует, что большая часть фотонов поляризуется в плоскости отражения 4 (рис. 25) и меньшая часть - в плоскости, перпендикулярной плоскости отражения. Схематически это можно показать в виде диаграммы 6 (рис. 25).
), отражаются, не меняя ориентации своей плоскости поляризации. Фактически, отраженные фотоны поляризуются в двух взаимно перпендикулярных плоскостях, одна из которых совпадает с плоскостью падения 3, а другая - перпендикулярна ей. Из описания Френеля следует, что большая часть фотонов поляризуется в плоскости отражения 4 (рис. 25) и меньшая часть - в плоскости, перпендикулярной плоскости отражения. Схематически это можно показать в виде диаграммы 6 (рис. 25). , то скорость центра масс фотона равна 1,4С. Это главный факт существования угла Брюстера (рис. 27, зависимость 3).
, то скорость центра масс фотона равна 1,4С. Это главный факт существования угла Брюстера (рис. 27, зависимость 3). , то рассеяние света наблюдается в основном в горизонтальной плоскости 7 (на экране - 8), а при виде сверху на сосуд, рассеянный свет очень слаб.
, то рассеяние света наблюдается в основном в горизонтальной плоскости 7 (на экране - 8), а при виде сверху на сосуд, рассеянный свет очень слаб.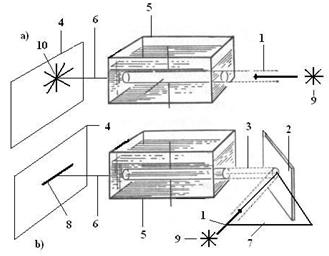
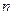 . Если
. Если 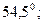

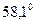 и
и 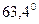 .
.
 при разной их поляризации:
при разной их поляризации:


