Есеп шығару үлгiлерi
Есеп 1. Екi нүктелiк заряд ауада бiр-бiрiнен 20 см арақашықтықта қандайда бiр күшпен өзара әсерлеседi. Осы зарядтардың майдағы өзара әсерлесу күштерi өзгермеуi (ауадағымен бiрдей болуы) үшiн олардың арақашықтықтары қандай болуы керек? Шешуi. «Ауа» ортаны «а» индексi және «май» ортаны «м» индексi арқылы белгiлеймiз. Кулон күшi мына формуламен анықталады:
мұнда ε – ортаның диэлектриктiк өтiмдiлiгi (енуi). Онда ауада зарядтардың өзара әсерлесу күшi келесi түрде өрнектеледi:
ал осы зарядтардың майдағы өзара әсерлесуi:
Есептiң шарты бойынша ауадағы Кулон күшi майдағы Кулон күшiне тең болуы керек, онда алатынымыз Fв = Fм, бұдан
немесе
Шарты бойынша ra = 20 см = 0,2 м; εa = 1, εм = 5. Одан алатынымыз, майда орналасқан зарядтар арасындағы арақашықтық, мынаған тең:
Жауабы: майдағы зарядтардың, өзара әсерлесу күшi ауадағыдай болуы үшiн, бiр-бiрiнен арақашықтығы 8,9 см болуы керек. Есеп 2. Тепе-теңдiк күйде болуы үшiн көлемi 9мм3 темiр В кiшкене бөлшектiң керосинге батырылған А шариктен (4.1 – сурет) қандай арақашықтықта орналасуы керек? Шарик заряды 7нКл, ал кiшкене бөлшектiң заряды – 2,1 нКл -ға тең. Темiрдiң тығыздығы 7800 кг/м3, керосиннiң тығыздығы – 800 кг/м3, керосиннiң диэлектриктiк өтiмдiлiгi (енуi) – 2,1. Шешуi. Кiшкене бөлшекке әсер ететiн күштердiң кескiнiн саламыз (4.2 – сурет). Кiшкене бөлшек тепе-теңдiкте болуы үшiн, оған әсер ететiн барлық күштердiң векторлық қосындысы нөлге тең болады:
Y осiне проекциялап, алатынымыз:
Архимед күшi Fарх = ρкgV, кулондық күш Fк = kq1q2/ ε r2, кiшкентай бөлшектердiң массасы мынадай белгiлi формула бойынша анықталады m = ε сV. Бұл өрнектердi (4.1) формулаға қойып, алатынымыз:
Арақашықтық терiс болмайтындықтан, ақырғы жауапты аламыз:
Өлшем бiрлiгiн тексерейiк:
Сандық мәндерiн қойып:
Жауабы: кiшкене бөлшек В тепе-теңдiк күйде болуы үшiн, ол зарядталған А шариктен 1 см қашықтықта болуы керек. Есеп 3. Нүктелiк зарядтар ортасында жатқан нүктедегi электр өрiсiнiң кернеулiгiн табыңыз q1 = 8·10-9 Кл, q2 = -6·10-9 Зарядтар арасындағы арақашықтық 10 см -ге тең. Шешуi. Бiрiншi зарядтың жасайтын электр өрiсi кернеулiгiнiң модулi мына формула бойынша есептеледi:
ал екiншi зарядтың жасайтын электр өрiсi кернеулiгiнiң модулi:
Өрiстердiң суперпозиция принципi бойынша қорытқы өрiстiң кернеулiгi мынаған тең
Бiзге қажет өрiс нүктесi, бiрi оң екiншiсi терiс зарядталған, екi зарядтың ортасында орналасқандықтан,
Алынған өрнектiң өлшем бiрлiгiн тексеремiз:
Жауабы: берiлген зарядтардың ортасында жататын нүктедегi электр өрiсiнiң кернеулiгi 5,04·10-4 В/м тең. Есеп 4. Кинетикалық энергиясы 10 кэВ электрон, горизонталь орналасқан, жазық конденсаторға ұшады. Конденсатор орамдарының арақашықтығы 1 см, ал пластина ұзындығы 10 см. Экран конденсатордан 20 см қашықтықта орналасқан. Электронның бастапқы жылдамдығы пластиналарға параллель бағытталған. Егер пластиналарға тұрақты 40 В кернеу берiлген болса, онда электронның экранда ығысуын табыңыздар. Шешуi. Конденсатор өрiсiндегi электрон электр күшiнiң әсерiнен қозғалады (4.3 – сурет). Электронның ауырлық күшi электр күшiнен көп кiшi болатындығынан, оны ескермеуге болады. Онда Ньютонның екiншi заңы бойынша алатынымыз:
Кернеулiк векторы пластиналарға перпендикуляр бағытталғандықтан, үдеудiң Х осiне проекциясы нөлге тең, ал Y осiне проекциясы eE/m тең. Бастапқы уақыт мезетiнде электронның кинетикалық энергиясы берiлген, сондықтан кинетикалық энергия өрнегiнен электронның бастапқы жылдамдығын табуға болады.
Х осi бойынша ығысуы бiрқалыпты және мына формула бойынша есептеледi:
Конденсатордағы ұшу кезiнде Y осi бойынша ығысуы мына формула бойынша есептеледi:
мұнда, tk – электронның конденсаторда болу уақыты. Y осi бойынша электронның жылдамдығы мынаған тең:
Конденсатор сыртында электрон X осi бойынша L = v0t1 қашықтыққа ұшып шығады, мұнда t1 – конденсатордан шығатын жерден экранға дейiнгi ұшу уақыты. Конденсатордан ұшып шыққаннан кейiн Y осi бойынша ығысуы мына формула бойынша есептеледi:
Электронның Y осi бойынша толық ығысуы – конденсатордың iшiндегi және сыртындағы Y осi бойынша ығысулардың қосындысынан тұрады:
(4.2) формуланы пайдаланып, конденсатор iшiнде және сыртында ұшу уақытын табуға болады:
Алынған өрнектердi yk и y1 анықталатын формулаларға қойып, алатынымыз:
Онда экранда электронның осы ауытқуы мынаған тең:
Мұнда пайдаланылған формула
Алынған өрнектiң өлшем бiрлiгiн тексеремiз:
Сандық мәндерiн қоямыз:
Жауабы: электронның экранда ығысуы 5·103 м. Есеп 5. Жазық ауа конденсаторының пластиналарының ауданы 100 см2. Олардың арасындағы арақашықтық – 5 мм. Пластиналардағы потенциалдар айырымы 300 В. Конденсаторды кернеу көзiнен ажыратқан кезде пластиналар арасындағы кеңiстiк эбонитпен толтырылады. Толтырылғаннан кейiн пластиналар арасындағы потенциалдар айырымы қандай болады? Толтырылғанға дейiн және одан кейiн конденсатор сыйымдылығы қандай? Шешуi. Жазық конденсатордың пластиналарындағы толтыруға дейiнгi және одан кейiнгi зарядтар – q1 және q2 болсын. Бұл жағдайда заряд тұрақты болып қалады, яғни q1 = q2 = q = const, бұдан шығатыны, пластинадағы зарядтың беттiк тығыздығы да тұрақты шама және мынаған тең:
Басқа жағынан, өрiс кернеулiгi жазық конденсатор потенциалының градиентпен байланысы келесi қатынаспен берiледi:
мұнда d – пластиналар арасындағы арақашықтық. Осылайша, алатынымыз: Толтырылғанға дейiн - Толтырылғаннан кейiн - Беттiк тығыздық пен пластиналар арасындағы арақашықтық өзгермейтiндiктен, алатынымыз:
бұдан: Сандық мәндерiн қойып, ε 2 = 2,6 екенiн ескерiп:
Конденсатордың электр сыйымдылығы оның орамдарының бiрiнiң зарядының орамдар арасындағы φ2 – φ1 = U потенциалдар айырымының қатынасына тең шама:
Жазық конденсатор үшiн
Осылайша, сандық мәндерiн қойып, алатынымыз:
Жауабы: пластиналар арасындағы потенциалдар айырымы эбониттi енгiзгеннен кейiн 115 В болады; конденсатор сыйымдылығы толтырылғанға дейiн – 1,77·10-11 Ф, толтырылғаннан кейiн - 4,6·10-11 Ф.
|

 ,
,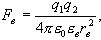
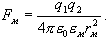
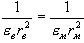 ,
,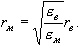 .
.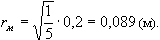 (м).
(м).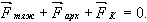
 (4.1)
(4.1)
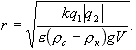

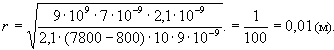 (м).
(м).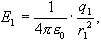 ,
,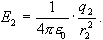 .
. .
. және
және 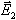 векторлары бiр бағытта бағытталған және олардың геометриялық қосындысы қарапайым өрнек түрiнде берiледi:
векторлары бiр бағытта бағытталған және олардың геометриялық қосындысы қарапайым өрнек түрiнде берiледi: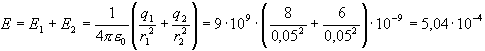
 .
.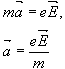

 . (4.2)
. (4.2)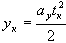 ,
, .
. .
. .
.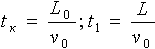

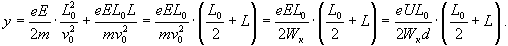 .
.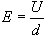 .
.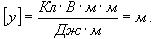 .
.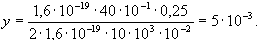 .
.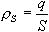 .
.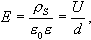 ,
, ,
, .
. ,
, .
. (В).
(В).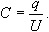 .
.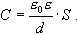 .
.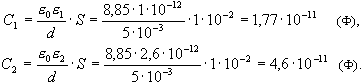 (Ф),
(Ф),


