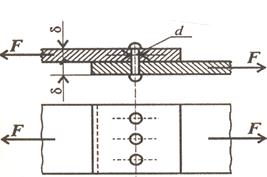
Definition. A line pencil is the set of straight line passing through a given point.
Arbitrarily varying the coefficient k in the equation All these straight lines constitute the line pencil centered at М0. A line pencil can also be specified by two equations of lines from this pencil (which determine of these lines) the common point М0(х0, у0) by the coordinates of its center. Suppose given intersecting straight lines with general equations
Consider the equations
where q1 and q2 undetermined multipliers, not both zero. Let us prove that, for any q1 and q2, the straight line (13) passes through the point М0 (х0; у0), which is the intersection point of the two given lines. The coordinates of the point М0 satisfy both equations
Consequently, the coordinates of М0satisfy equation (13), i.e.,
Thus, the point М0 belongs to the straight line (13) for any q1 and q2; but for particular values of q1 and q2, we obtain some straight line from the pencil. In practice, it is more convenient to write an equation of a pencil with one parameter l:
Example. Draw a straight line through the intersection point of the lines х+у–3=0 and 2х–у+5=0 so that it passes through the point М(3;5). Let us write the equation of the pencil of lines according to the formula. To find the required line, we must find the value of the parameter l:
We substitute the coordinates of the point М(3;5) into the equation of the pencil:
Substituting l in to the equation of the pencil, we obtain the required equation:
|

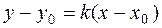 of a line passing through a point М0(х0,у0), we obtain equations of all straight lines passing through the point with coordinates х0, у0.
of a line passing through a point М0(х0,у0), we obtain equations of all straight lines passing through the point with coordinates х0, у0. ,
,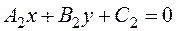 .
. , (13)
, (13) ,
,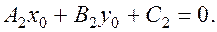
 .
. .
.
 ,
, .
. ;
; 
 .
.