Straight Lines in the PlaneThe equation of a straight line with a slope. Given a straight line, we denote the angle between this line and the x–axis by j and the interval cut out by the line on the x-axis by b.
у М(х;у)
B j
0 x
Definition. The slope tangent of the angle between a straight line and the x –axis is called the slope of the line and denoted by k =tan j. Suppose that k is the slope of a line and b is its y –intercept. The equation of a straight line with a slope has the form
y
M(x;y)
M0(x0;y0) N
0 x By analogy with the equation of a straight line with a slope consider the triangle М0MN; we have consideration or Thus, the required equation is y – y 0 = k (x–x 0).
The equation of a straight line passing through two points. Suppose that a straight line passes through two points М 1(х 1; у 1) and М 2(х 2; у 2).
M(x;y)
M2(x2;y2) M1(x1;y1) 0 x
Take a point M(x,y) on the line and consider the vectors
These two vectors The collinearity condition is the proportionality of the perspective coordinates, i.e.,
This is the equation of a straight line passing through the two given points. Example. Write an equation of the straight line passing through the points М1 (2;–5) and М2 (3;2) and find k and b. Using formula (10), we obtain
Thus the equation of the straight line is y=7x–19, and the slope and the y –intercept are k=7, b= –19.
|
y-b
b N
.
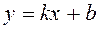The equation of a straight line with given slope passing through a given point. Suppose that a straight line passes through a point М0(x0,y0) and has slope k.
φ
φ
for any point М on the under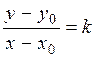
.
y
and 
.
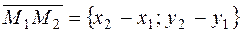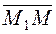и 
lie on the same straight line and are collinear.
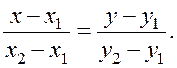(10)
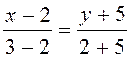Þ 7 x –14= y +5.
