The second method for calculating the rank of a matrix.
The elementary transformations of matrices include: - permutation of columns or rows in a matrix, - multiplication and division of the elements of a row or a column by a nonzero number, - linear combination of rows (columns). The elementary transformations of a matrix do not affect its rank. Theorem. The rank of a matrix equals the number of nonzero elements on the main diagonal of any diagonal matrix obtained by elementary transformations from the initial matrix. (Without proof). In the Gauss-Jordan method, only operations on rows are allowed; in calculating rank, we may operate on both rows and columns.
We interchanged the first and second rows and obtained zeroes in the first column by using the second row. Then, using the first column, which has only one nonzero element, we obtained zeroes in the first row. Interchanging the second and third rows and using the new second row, we obtain zeroes in the second column, etc.
Kronecker-Capelli theorem. Consider the system of m linear equations with n unknowns:
Let us compose the principal and augmented matrices of this system:
Theorem. A system of equations is consistent if and only if the rank of the augmented matrix
Corollary 1. Any homogeneous system of equations
is consistent. Indeed, it suffices to take bi =0 for all i. Corollary 2. System of equations (8) is consistent and has a unique solution if and only if the ranks of the matrices are equal and coincide with the number of unknowns. Example. Determine whether the following system is consistent:
|

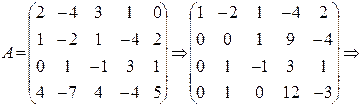 …
…

 (8)
(8)
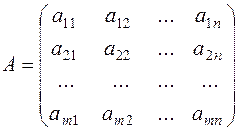 ;
; 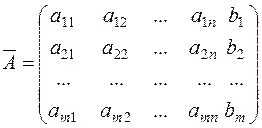 .
.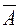 equals that of the principal matrix А, i.e.,
equals that of the principal matrix А, i.e., . (9)
. (9)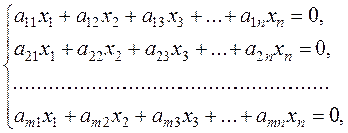
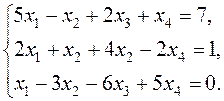
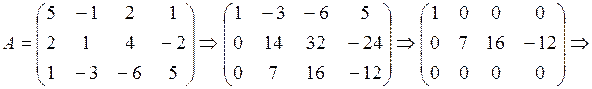
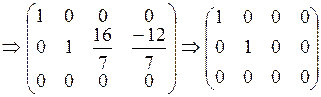 ,
,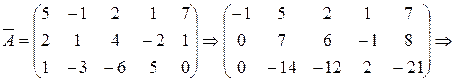
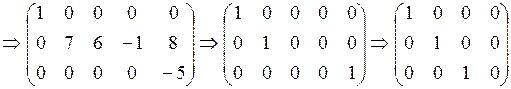 ,
,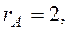
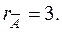 The system is inconsistent.
The system is inconsistent.


