Rank of a MatrixDefinition. Consider two systems
These systems are said to be linearly dependent if
where k 1 If these relations hold only for k 1 = 0 and k 2=0, then these two systems are linearly independent. Consider an
Definition. The maximal number of linearly independent rows in the matrix А is called the rank of this matrix. The maximal number of linearly independent rows equals the maximal number of linearly independent columns. Definition. A k th-order minor of a matrix А is the determinant consisting of the elements of arbitrarily chosen k columns and k rows. Theorem. If all k th - order minors of a matrix are zero, then all (k+j)th - order minors are also zero. Theorem. The rank of a matrix equalsthe maximal order of a nonzero minor. The first method for calculating the rank of matrix (the bordering method). (а) The method is to pass lower-order minors to higher-orders minors. (b) Choose a nonzero minor and border it by a column and a row. (c) If all of the bordered minors are zero, then the rank of the matrix equals the order of the nonzero k th-order minor:
Example. Calculate the rank of a matrix
We have
Since all of forth-order minors equal zero and the determinant of third order does not equal zero, it follows that
|
;
.
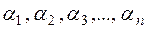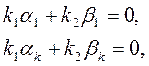
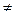0 or k 2 
matrix
.
.
.
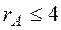, i.e., can the rank not be larger than 4.
,
,
, 
.
.
