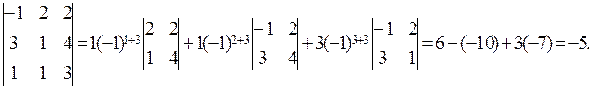Algebraic complements and minors.
Definition. The minor of an element аij is the determinant of order lower by one consisting of the elements that remain after the deletion of the i th-series and j th - column, which intersect in aij. For example, the minor of the element a 32 is
Definition. The algebraic complement of an element аij is the minor of aij multiplied by -1 raised to the proper equal to the sum of the numbers of the row and the column intersecting in the given element:
9. A determinant equals the sum of products of all elements of any lines and the corresponding algebraic complements.
For a k th order determinant, we can write property 9 in the form of expansion along the k th-column:
10. The sum of the products of the elements of any line and the algebraic complements of the corresponding elements of a parallel line equals zero:
= Examples. Let us expand the following determinant along the third row:
|



 ;
; is the minor of
is the minor of  .
. .
.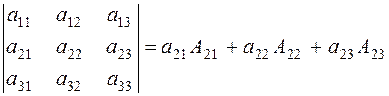 .
.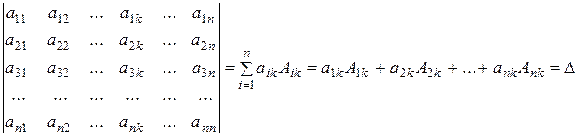 .
.