Determinants of second and third order
Consider the system of two linear algebraic equations in two variables
where a 11, a 12, a 21, and a 22 are coefficients, b 1 and b 2 are right-hand sides, and x 1 and x 2 are unknowns. Let us solve this system by the school method of algebraic addition, namely, multiply the first and second equations by а 22 and – a12, respectively, and sum the results. The coefficient of х 2 will vanish. The remaining unknown, х 1, is found as follows: x 1(a 11 a 22– a 12 a 21)= b 1 a 22– a 12 b 2,
In a similar manner, multiplying the first equation of the system by – а 21, the second by а 11 , and summing the resulting equations term by term, we obtain
Definition. The number
is called a determinant of second order. The numbers a 11 ,a 12 ,a 21 and a 22 are called the elements of the determinant. The second-order determinant is equal to the product of the elements of the main diagonal minus the product of the elements of the secondary diagonal. Example. Find the determinants
The unknowns х 1 and х 2 of the linear system (1) are determined by the formulas
The determinant Example.
A third-order determinant is the number
The simplest method for calculating a third-order determinant is the triangle rule. The main diagonal of the determinant is the line containing the elements a 11, a 22 and a 33. The secondary diagonal is the line containing the elements a 13, a 22 and a 31. The products of the main diagonal elements and of the elements contained in the triangles shown below are summed with the plus sign:
The products of the secondary diagonal elements and of the elements contained in the triangle shown below are summed with the minus sign:
Another method forcalculating a third-order determinant is as follows. We write the first columns on the right of the determinant, and sum the products of the elements of the main diagonal and of the two parallel diagonals with the plus sign. Then we add the products of the elements of the secondary diagonal and of the two parallel diagonals with the minus sign + + +
– – – As a result, we obtain the determinant. Example. Calculate the determinant by the triangle rule:
The determinant of order n is the expression
An n th-order determinant contains n 2 elements. The subscript, i, indicates the number of the row and the second subscript j, indicates the number of the column containing the element аij.
Properties of determinants. All determinants of any order have the same properties. For simplicity, we give only properties of third-order determinants. 1. The interchange of rows and columns in a determinant does not change its value:
2.The interchange of two rows (columns) in a determinant changes only the sign of the determinant:
3. If all elements of any lines (a row or a column) are zero, then the determinant is equal to zero:
The proof follows from the triangle rule. 4. A determinant containing two equal lines is equal to zero:
5. The common multiplier of all elements of a line can be factored out:
6. A determinant containing two proportional lines, is equal to zero:
7. If each element of some line is the sum of two terms, then such a determinant equals the sum of two determinants, which contain these terms instead of the elements of the lines.
8. A determinant does not change under the replacement of any line by the sum of this line and any parallel line multiplied by some number.
|

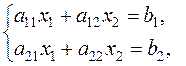 (1)
(1)
 ,
,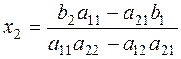
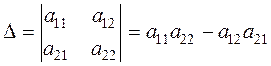
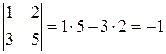

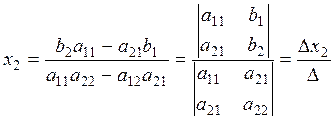
 is called the principal determinant of the system; it is formed by the coefficients of the unknowns.
is called the principal determinant of the system; it is formed by the coefficients of the unknowns. 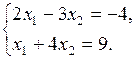
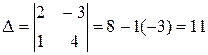 ,
,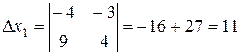 ,
,  ,
,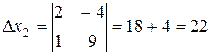 ,
,  .
.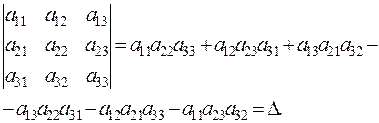














 .
.


 .
.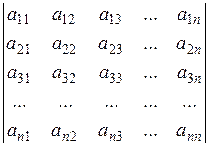 .
.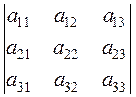 =
= 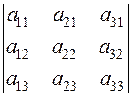 (the transposed determinant).
(the transposed determinant).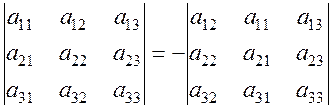 .
.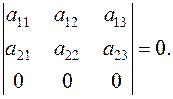
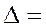
 =0.
=0. .
.
 .
.


