Matrices and Operations on ThemDefinition. A matrix of size
m is the number of rows, n is the number of columns, and аij is an element of the matrix. If m = n, then the matrix is square. A null-matrix is a matrix А, in which all elements are zero:
Definition. A square matrix А is said to be diagonal if its main diagonal may contain nonzero elements, but all nondiagonal elements are zero:
Definition. The identity matrix is the diagonal matrix with ones on the diagonal:
Definition. Matrices of the same size are equal if their respective elements are equal. Two matrices of the same size can be added (elementwise):
Any matrix can be multiplied by any number all elements of the matrix should be multiplied by this number):
Subtraction is defined as А–В=А +(– 1) В. Two matrices can be multiplied only if the number of columns in the first matrix equals the number of rows in the second matrix. An
We obtain a matrix of size Multiplication of matrices is not commutative, and sometimes even impossible: АВ
|
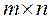is a table written in parentheses or between two pairs of parallel lines:
,
; 
.
.
.
.
.
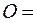
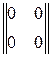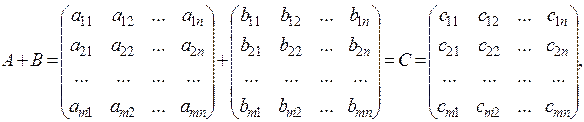
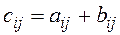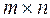matrix is multiplied by an 
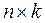matrix as follows:
.
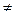ВА.
