Inverse Matrices
Definition. A square matrix is said to be nondegenerate, if it has nonzero determinant. Consider the identity matrix
Definition. The inverse matrix for А is the matrix А –1for which
Inverse matrices exist only for nondegenerate matrices. The first method for finding the inverse matrix. Consider a square nondegenerate matrix of size n
Let us compose the square matrix
where the Аij are the algebraic complements of аij. The matrix А * is called the adjoint matrix. Let us multiply А by А * :
The remaining elements of the first row in the new matrix are the sum of the products of the elements of the first row and the algebraic complements of the parallel rows. According to property 10, they equal zero. The same is true for the elements of the second row, except the second element, which are the sum of the products of the elements of the second row by the algebraic complements of the first, third,... rows. To obtain the identity matrix from this diagonal matrix, we must divide it by the determinant
consequently,
Example. Find the inverse matrix for the matrix
Let us verify condition (11) from the definition of the inverse matrix:
The second method for finding the inverse matrix. This method is similar to the Gauss-Jordan method. Applying the Jordan transformations to the rows of the principal matrix, we reduce it to the identity matrix, and the identity matrix added to it becomes the inverse matrix.
Example.
|

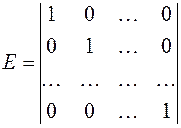 .
.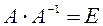 или
или 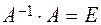 . (11)
. (11) n
n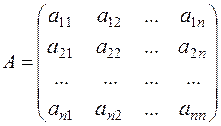 .
.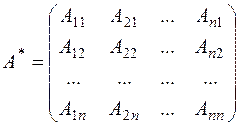 ,
,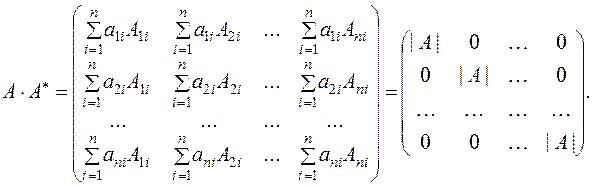
 , i.e.,
, i.e., ;
; ,
, 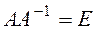 ,
,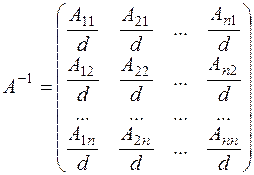 . (12)
. (12)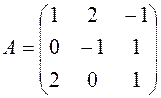 ,
, 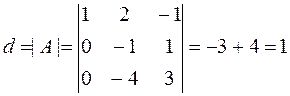 ,
,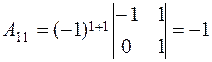 ,
, 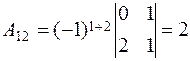 ,
, ,
, 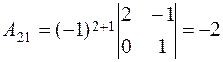 ,
,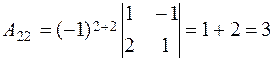 ,
,  ,
,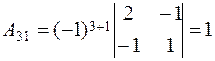 ,
,  ,
, ,
, 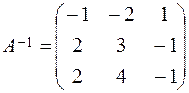 .
. .
.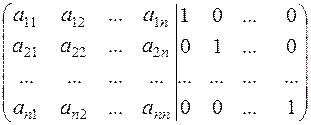
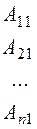
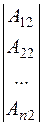

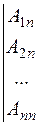

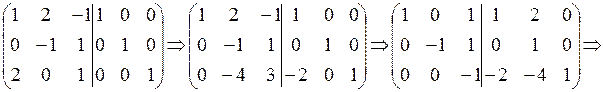
 .
.


