Analytic Geometry in the Plane
Consider the Cartesian rectangular coordinate system in the plane. Taking the projection of any point М1 on the x and y coordinatewe obtain two numbers x=a1 and y=b1. Take two numbers a2 and b2 plot a2 on the x -axis and b2 on the y -axis. Having drawn two straight lines parallel to the coordinate axes through these points we find obtain a point M 2 in their intersection.
0
The distance between two points. Let us find the distance between two points М 1 and М 2 in the plane.
M2(x2;,y2) d M1(x1;y1) 0 x Compose the vector The length of this vector is defined by
This is the distance between the two given points. Example. Find the distance between the two points А (2;3) and В (–4;11). Using the above formula, we obtain
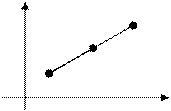
Division of an interval in a given ratio. Suppose given an interval М 1 М 2. Let us find the coordinates a of point М on the interval for which
y M2(x2,y2) M(x,y) M1(x1,y1) 0 x This gives the x coordinate; y is found in a similar way:
To obtain a formula for the midpoint of the interval, we take l =1:
Example. Given the two points М 1(–2;4) and М 2(6;2), find the midpoint of the interval М 1, М 2.
М 2
|
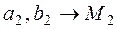
y
.
.
.
.
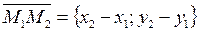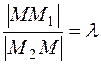Compose the vectors 
and 
.
; 
.
; 
.
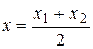М 1 
,
.
