Matrix Method for Solving Systems of EquationsConsider a system of n equations with n unknowns:
Let us find a solution of system (13), by using matrices. The matrix method applies only where the number of equations equals that of unknowns. Let us write system (13) in matrix form; for this purpose we introduce, principal matrix А, the column matrix Х, and the column matrix of free terms В:
Then system (13) can be written in the form of the matrix equation АХ = В.
Two matrices of the same size are equal if and only if each element of one matrix equals the corresponding element of the other matrix. To find the matrix Х, we multiply both sides of the matrix equation by the inverse matrix А -1 on the left
Since
Thus, to solve the given system of equations by the matrix method, it is sufficient to find the inverse matrix А -1 and multiply it by В on the right. Example. Solve the following system of equations by the matrix method:
Let us write the system in matrix form:
Applying (14), we obtain
The principal matrix is nondegenerate, and its determinant equals d =6. Now, let us find the inverse matrix:
The solution of the system is
Thus, the solution of the system is x1 = –1, x2 = –2, x3 =2.
|
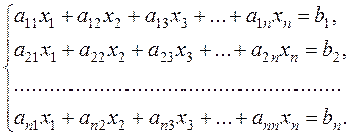(13)
.
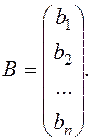
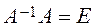is the identity matrix, we have
. (14)
.
.
.
.
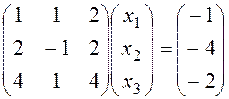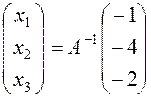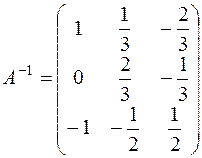