The Normal Equation of a Straight Line
The position of a straight line in the plane is completely determined by the distance from the line to the origin of coordinates, i.e., the length of the perpendicular
Т
0 x
Let us construct an equation of a straight line from the length of the perpendicular р and its angle a with the x-axis. To this end we take an arbitrary point М on the line and find the projection of the vector The point М belongs to the given line if and only if
In terms of inner product of vectors, we have
Considering this product, we obtain
Equation (14) is the normal equation of the line in vector form. To pass to coordinates, note that the projections of the unit normal vector are
where a is the angle between this vector and the axis ОX. Let the projections of the radius-vectors
This equation is called the normal equation of the straight line. It is clear from equation (15) that the “normality” conditions are (1) (2) –р<0 (the free element is negative). Example. Which of the following equations are normal? (a) (b) (c)
A normalizing factor. Suppose given a general equation of a straight line given:
Definition. The normalizing factor is the number such that the equation multiplied by this number is normal. Let us multiply the general equation of a straight line by number
By definition, if this equation is normal, then the two normality conditions hold:
Removing parentheses, we obtain
extracting the root, we see that the normalizing factor is
the sign of the fraction is opposite to that of the free element of the general equation. Example. Reduce the equation 8х–6у+5=0 to the normal form. We find the normalizing factor
and multiply the equation by this factor term by term:
|

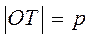 from the origin to the fight line, and the unit normal vector
from the origin to the fight line, and the unit normal vector y
y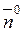 α M
α M on the unit normal vector
on the unit normal vector 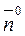 .
. . (*)
. (*)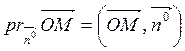 .
. . (14)
. (14) ,
,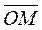 on the axes ОХ and ОУ are х and у, respectively. The inner product formula (14) implies
on the axes ОХ and ОУ are х and у, respectively. The inner product formula (14) implies . (15)
. (15)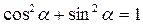 (the sum of squared coefficients of х and у equals 1);
(the sum of squared coefficients of х and у equals 1); ,
,  , this is not a normal equation;
, this is not a normal equation;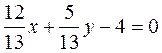 ,
, 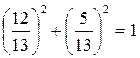 and –4<0, this is a normal equation;
and –4<0, this is a normal equation;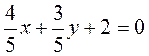 ,
,  but 2>0, this is not a normal equation.
but 2>0, this is not a normal equation.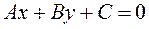 .
. m:
m: .
. ;
; 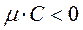 .
.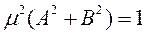 ;
; ;
;
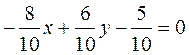 or
or  .
.


