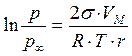Тиск насиченої пари над викривленою поверхнею
Додаткова зміна енергії Гіббса, що пов’язана з дисперсністю, дорівнює:
р, р∞ - тиск пари над викривленою і рівною поверхнею, відповідно. Підставивши рівняння (3.17) в (3.18) одержуємо:
Рівняння (3.20) називають рівнянням Кельвіна (Томсона) Тиск пари над краплею буде тим більший, чим більша кривизна поверхні, або чим менший радіус краплини. У випадку від’ємної кривизни, яка виникає в капілярах при змочуванні тиск пари над викривленою поверхнею зменшується зі збільшенням кривизни поверхні або зі зменшенням радіуса. Тому конденсація рідини в капілярі відбувається при тиску меншому ніж над рівною поверхнею і рівняння Кельвіна часто називають рівнянням капілярної конденсації.
Приклад 3.3 Обчисліть тиск насичених парі над краплями води з дисперсністю 0,1 нм-1 при температурі 293К. Тиск парів води над плоскою поверхнею при цій температурі 2338 Па, густина води 998 кг/м3, поверхневий натяг 72,7 мДж/м2. Вплив кривизни поверхні на тиск насиченої пари виражається рівнянням Кельвіна
ln(p/p∞) = (2∙0,0727∙18∙10-3∙2∙108)/(8,314∙293∙988) = 0,21 p/p∞ = exp(0.21) =1,23; p = 1,23∙2338 = 2875 Па
Приклад 3.4 Обчисліть тиск пари над увігнутим меніском в капілярі радіусом 1 мкм при 293 К. Кут змочування дорівнює нулю. Густина води 0,998 г/см3, тиск пари над макрофазою 2338 Па, поверхневий натяг води 72,75 мДж/м2.
ln(p/p∞) = (2∙72,75∙10-3∙18∙10-6)/(8,314∙293∙1∙10-6) = -1,075∙10-3 p/p∞ = exp(-1,075∙10-3) =0,9989 p = 0,9989∙2338 = 2335 Па
|

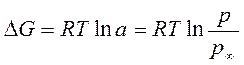 , де (3.18)
, де (3.18)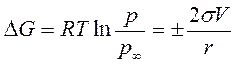 (3.19)
(3.19) (3.20)
(3.20)