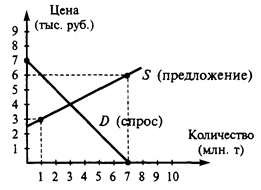
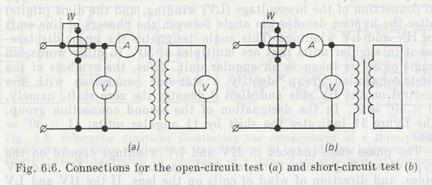
Open-Circuit and Short-Circuit Tests
These tests enable experimental measurements of the desired quantities. In the open-circuit test (Fig. 6.6a), the transformer secondary is open and carries no current (I 2 = 0), while the secondary re ceives power from an ac source and carries an exciting current, i.e. an open-circuit (no-load) current /0. In high-power transformers, the exciting current can reach 5 to 10% of the rated value. In low-power transformers, this current amounts to 25-30% of the primary current rating. The open-circuit current /0 produces a magnetic flux in the transformer core. The transformer draws the reactive power from the circuit to establish the magnetic flux. As for the active power absorbed by the transformer, this power is spent on offsetting the core loss due to hysteresis and eddy currents. Since the reactive power at no-load is much higher than the active power, the power factor cos φ is fairly small and is commonly equal to 0.2 to 0.3.
With the secondary shorted out, the short-circuit current flows through the secondary circuit, which is much higher than the rated value since the transformer resistance is very small. This high current heavily heats up the windings and can render the transformer inoperative if the protective system does not disconnect it from the supply. In the short-circuit test (Fig. 6.66), the secondary is short-circuited, so the voltage across its terminals is equal to zero. The primary is connected to a power source of a reduced potential difference that is enough to cause the rated currents to circulate in the windings. This reduced potential difference used in the short-circuit test is known as the impedance voltage vsc, usually expressed in percent of the rated voltage. Under short-circuit conditions, the resistance, reactance, and impedance are given as Rsc=Psc/I2, Xsc= In defining the performance of a three-phase transformer, we should substitute the phase values of voltage, current, and power into the above equations.
The impedance voltage and its active and reactive components expressed in percent of the rated voltage are: vsc = IrZscVr x 100, va = IrRscVr x 100, and vx = IrXsc/Vr x 100, where Vr and Ir are the rated voltage and rated current of the primary.
|

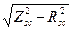 , and Zsc=Vsc/I, where Vsc, I, and Psc are the voltage, current, and power measured in the primary circuit.
, and Zsc=Vsc/I, where Vsc, I, and Psc are the voltage, current, and power measured in the primary circuit.