Понятие спрямляемой дуги.
В школьном курсе математики рассматривался вопрос о вычислении длин отрезков прямой, длины окружности, а также различных её частей. В приложениях математики возникает потребность в вычислении длин дуг произвольных кривых. Но, чтобы вычислить длину произвольной кривой, надо быть уверенным в том, что рассматриваемая кривая имеет конечную длину. В средней школе длиной окружности называют предел последовательности периметров вписанных в окружность правильных многоугольников (при неограниченном удвоении числа сторон). Однако это определение неприменимо к произвольным кривым. Дадим общее определение понятия длины кривой. Пусть задана жорданова кривая Г1:
a Напомним, что функции t0, t1,…, tn: a = t0 < t1 < … < tn = в. Каждому числу t соответствует точка Мк ( Определение. Жорданова кривая (1) называется спрямляемой (имеющей длину), если множество
Докажем, что длина спрямляемой кривой обладает свойством аддитивности. Пусть жорданова кривая Γ разбита на кривые В самом деле, пусть γ – любая ломаная, вписанная в кривую Γ, и пусть М – точка, разбивающая Γ на Поэтому
Это неравенство показывает, что число
Объединяя
А это и значит, что
|

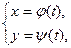 (1)
(1)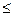 t
t 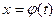 и
и 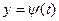 непрерывны на отрезке. Разобьём отрезок [ а;в ] на части числами
непрерывны на отрезке. Разобьём отрезок [ а;в ] на части числами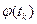 ,
,  ) кривой Г. Проводя отрезки М0М1, …, Mn-1Mn, получим ломаную линию ɣ, вписанную в кривую Г. Обозначим её длину через l (ɣ).
) кривой Г. Проводя отрезки М0М1, …, Mn-1Mn, получим ломаную линию ɣ, вписанную в кривую Г. Обозначим её длину через l (ɣ). длин вписанных в эту кривую ломаных γ ограничено сверху. Точная верхняя граница множества
длин вписанных в эту кривую ломаных γ ограничено сверху. Точная верхняя граница множества 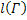 :
: . (2)
. (2)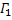 и
и  . Если эти кривые спрямляемы, то кривая Γ спрямляема, причем
. Если эти кривые спрямляемы, то кривая Γ спрямляема, причем 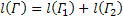 .
. и
и  . Добавляя эту точку к вершинам ломаной γ, получим ломаную
. Добавляя эту точку к вершинам ломаной γ, получим ломаную  , длина которой не меньше длины ломаной γ,
, длина которой не меньше длины ломаной γ,  . Но ломаная
. Но ломаная  и
и  , вписанных соответственно в кривые
, вписанных соответственно в кривые 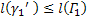 и
и 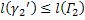 .
.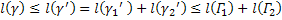 .
.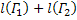 является одной из верхних границ для множества
является одной из верхних границ для множества  найдутся ломаные
найдутся ломаные 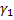 и
и 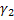 , вписанные в
, вписанные в 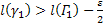 и
и  .
.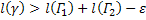 .
.


