Достаточное условие спрямляемости прямой.
Назовем жорданову кривую Γ:
регулярной, если функции φ и ψ имеют на отрезке Теорема 1. Всякая регулярная жорданова кривая Γ спрямляема. Доказательство. Разобьем отрезок
Но по теореме Лагранжа найдутся такие
и поэтому
 . .
Значит, длина всей ломаной выражается формулой
По условию производные
Но тогда
а потому в силу (3)
Поскольку
Поэтому кривая Γ спрямляема. Отметим, что из равенства (3) вытекает также оценка длины ломаной снизу:
где α и β – наименьшие значения для Из неравенств (4) и (5) вытекают аналогичные неравенства для длины кривой: (6) (7) Неравенство (7) следует из неравенства (5) и из того, что lкр
|

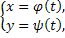
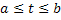 ,
, непрерывные производные. Справедлива следующая теорема.
непрерывные производные. Справедлива следующая теорема.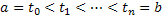 и впишем в кривую Γ ломаную, соответствующую этому разбиению. Рассмотрим одно звено
и впишем в кривую Γ ломаную, соответствующую этому разбиению. Рассмотрим одно звено  этой ломаной,
этой ломаной,  ,
,  (рис. 49). Длина этого звена равна
(рис. 49). Длина этого звена равна
 .
. и
и  , что
, что ,
,
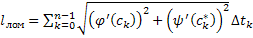 . (3)
. (3) и
и 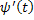 непрерывны на отрезке
непрерывны на отрезке  и
и 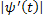 на отрезке
на отрезке  ,
,  .
. ,
, 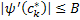 ,
,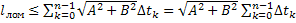 .
. , то для всех ломаных, вписанных в кривую Γ,
, то для всех ломаных, вписанных в кривую Γ, (4)
(4) , (5)
, (5)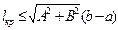 ,
, .
.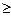 lлом. Чтобы доказать неравенство (6), заметим, что в силу неравенства (4)
lлом. Чтобы доказать неравенство (6), заметим, что в силу неравенства (4) 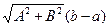 является одной из верхних границ для длин вписанных в Г ломаных, число lкр – точная верхняя граница для этих длин, т.е. наименьшая из верхних границ. Отсюда и следует неравенство (6).
является одной из верхних границ для длин вписанных в Г ломаных, число lкр – точная верхняя граница для этих длин, т.е. наименьшая из верхних границ. Отсюда и следует неравенство (6).


