площадь поверхности вращения.
Пусть даны прямая m и кривая Г, лежащая в одной плоскости с m и расположенная по одну сторону от этой прямой. При вращение кривой Г вокруг оси m получается поверхность
Начнём со случая, когда Г – отрезок, один конец которого отстоит от m на r, а другой на R. (рис.58). Тогда, как доказывается в школьном курсе геометрии, площадь поверхности вращения (боковой поверхности усечённого конуса) выражается формулой Р( В этом случае при r (1) 2 Таким образом, боковая поверхность конуса заключена между произведением длины образующей на длину наименьшей окружности и произведением длины образующей на длину наибольшей окружности. То же самое неравенство будет иметь место и при вращении любой ломаной линии, расположенной по одну сторону от оси вращения: (2) 2 где r и R – наименьшее и наибольшее расстояния точек ломаной от оси m, l – длина ломаной. Для доказательства достаточно применить неравенство (1) к каждому звену ломаной, сложить полученные результаты и учесть, что Естественно потребовать, чтобы неравенства (2) выполнялись для любой спрямляемой кривой. Кроме того, потребуем, чтобы площадь поверхности вращения обладала свойством аддитивности: при разбиении дуги Г на части ɣ0, …, ɣn-1 должно выполняться равенство где Если применить к каждой части где lк= l( ɣк) – длина дуги ɣк, а rк и Rк – наименьшее и наибольшее расстояния точек этой дуги ɣк от оси вращения. Складывая эти неравенства и учитывая требование аддитивности, получаем, что (4) 2 Иными словами, площадь поверхности вращения должна разделять множества
Именно это требование мы и примем за определение площади поверхности вращения. Если Г – плоская спрямляемая кривая, лежащая по одну сторону от оси m, то площадью поверхности
Докажем сейчас, что это число существует и единственно, а затем выведем для него выражение в виде интеграла. Выберем на плоскости систему координат, такую, что ось абсцисс совпадает с осью вращения. Зададим параметризацию кривой Г, выбрав в качестве параметра длину l дуги Ам, соединяющей в заданном направлении фиксированную точку А кривой Г с произвольной точкой М этой кривой (рис.59). Тогда rк иRк будут наименьшими и наибольшими значениями ординаты для точек части ɣк. Поэтому суммы, стоящие в неравенствах (4) слева и справа, являются не чем иным, как суммами Дарбу для интеграла 2 (5) Р( Из формулы (5) получаются различные частные случаи в зависимости от того, как задана кривая Г. Если она задана параметрически:
t0 и формула (5) принимает вид: (6) Р( (когда l меняется от 0 до L, переменная t меняется от t0 до Т). В частности, если кривая Г задана явным уравнением y=f(x), а (7) Если кривая Г задана в полярных координатах уравнением (8) Р = 2 Пример 1. Найдём площадь поверхности шара радиуса R. Решение. Поместим начало координат в центр шара. Будем рассматривать поверхность шара как поверхность, полученную в результате вращения полуокружности х2+у2=R2 вокруг оси Ох. Тогда площадь поверхности шара найдётся по формуле Р = Так как Р = Найдя
получим:
|

 , площадь которой мы хотим сначала определить, а потом вычислить.
, площадь которой мы хотим сначала определить, а потом вычислить.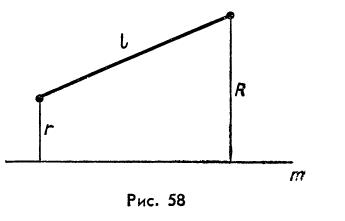
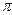 (r + R) l.
(r + R) l.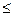 R имеем:
R имеем: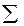 lk = l и для любого звена имеем r
lk = l и для любого звена имеем r 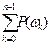
 - при вращении части ɣк.
- при вращении части ɣк. rк lк
rк lк  и
и  .
.
 (l) dl, где через L обозначена длина всей кривой Г. Поскольку функция y (l) непрерывна в силу непрерывности кривой Г, то существование и единственность числа, разделяющего эти суммы Дарбу, вытекают из теоремы существования интеграла от непрерывной функции. При этом мы доказали, что площадь поверхности вращения, т.е. число Р(
(l) dl, где через L обозначена длина всей кривой Г. Поскольку функция y (l) непрерывна в силу непрерывности кривой Г, то существование и единственность числа, разделяющего эти суммы Дарбу, вытекают из теоремы существования интеграла от непрерывной функции. При этом мы доказали, что площадь поверхности вращения, т.е. число Р(


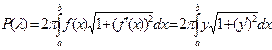 .
. где
где 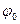
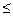
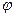
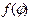 имеет непрерывную производную
имеет непрерывную производную 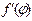 на [
на [ 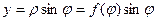 , а
, а 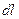 =
= 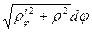 , получим:
, получим: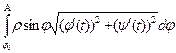 .
.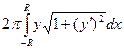 .
. - функция чётная, то
- функция чётная, то .
.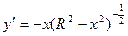 и вычислив сумму
и вычислив сумму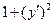 =
= 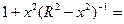
 ,
,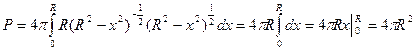 .
.


