Внешние, внутренние и граничные точки плоских множеств.
Вычисление площадей плоских фигур Внешние, внутренние и граничные точки плоских множеств. Выше мы неоднократно использовали понятие площади плоской фигуры, опираясь на его интуитивное толкование. В этом параграфе мы дадим определение понятия площади плоской фигуры, установим свойства площадей и опишем класс фигур, имеющих площадь. Для этого введем несколько понятий, относящихся к плоским фигурам, т.е. к множествам, состоящим из точек плоскости. Напомним, что открытым кругом с центром a и радиусом r называют множество U (a, r) точек плоскости, расстояние которых от точки a меньше r. Любой открытый круг с центром a называют окрестностью точки a. Пусть на плоскости задано некоторое множество X. Назовем точку a этого множества внутренней, если существует окрестность этой точки, целиком содержащаяся в X. Точку плоскости называют внешней точкой для этого множества, если у нее есть окрестность, не содержащая ни одной точки множества X. Наконец, точки плоскости, не являющиеся ни внутренними, ни внешними для множества X, называют граничными точками этого множества. Граничные точки могут как принадлежать множеству X, так и не принадлежать ему. Совокупность граничных точек множества X образует границу этого множества. Если все граничные точки множества X принадлежат этому множеству, то его называют замкнутым, а если ни одна граничная точка не принадлежит множеству X, то его называют открытым. На рисунке 20 изображен квадрат. Точка e является внутренней для этого квадрата, точка f - внешней, а точка g - граничной. Граница квадрата состоит из отрезков ab, bc, cd и da. В дальнейшем будем говорить, что фигуры F и G налегают друг на друга, если у них есть хоть одна общая внутренняя точка (рис. 21).
Если фигура F является объединением попарно не налегающих друг на друга фигур 2. Квадрируемые области. Перейдем к определению понятия площади. Выберем на плоскости прямоугольную декоративу систему координат Oxy. Назовем прямоугольник допустимым, если его стороны параллельны осям координат, причем не будем исключать и вырожденные прямоугольники, т.е. прямоугольники, у которых длина одной или обеих сторон равна нулю. Подмножество F плоскости, которое можно разбить на конечное число допустимых прямоугольников, назовем ступенчатой фигурой (рис. 23). Очевидно, что объединение и пересечение двух ступенчатых фигур являются ступенчатыми фигурами. Назовем площадью допустимого прямоугольника F произведение длин его сторон:
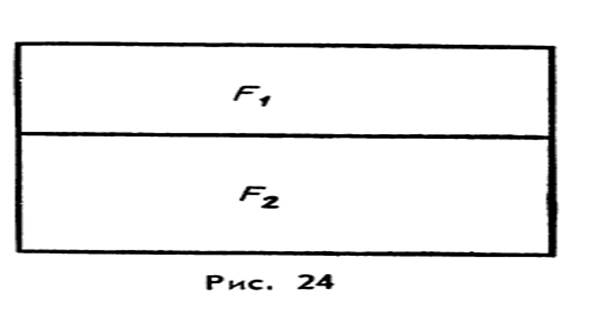
При этом площадь вырожденного прямоугольника равна нулю. Очевидно, что если прямоугольник разбит на два прямоугольника (рис. 24), F =
Вообще, если прямоугольник F разбит на конечное число прямоугольников Кроме того, если прямоугольник Отметим, что квадрат со стороной, равной 1, имеет площадь, равную 1. Определим далее площадь ступенчатой фигуры. Пусть ступенчатая фигура F разбита на прямоугольники Положим тогда:
Одна и та же ступенчатая фигура может разбиваться на прямоугольники различными способами. Легко доказать, что её площадь не зависит от способа разбиения. Мы определили функцию а) если ступенчатые фигуры S ( б) если ступенчатая фигура Из свойства а), в частности, следует, что если Совокупность ступенчатых фигур не охватывает таких фигур, как, например, треугольник, параллелограмм общего вида, круг, эллипс. Даже повернутый прямоугольник уже не является ступенчатой фигурой (стороны ступенчатой фигуры параллельны осям координат). Поэтому надо распространять понятие площади на более широкий класс фигур. Возьмем на плоскости фигуру A и поставим ей в соответствие два числовых множества. Множество
Введем следующее определение. Определение. Фигура A называется квадрируемой (имеющей площадь), если соответствующие ей числовые множества разделяются единственным числом. Это единственное число Применяя критерий единственности разделяющего числа, получаем необходимое и достаточное условие квадрируемости фигуры A: Для того, чтобы фигура A была квадрируемой, необходимо и достаточно, чтобы для любого
Отметим, что граница фигуры А лежит в области, заключённой между границами ступенчатых фигур F1 и F2. Эта область сама является ступенчатой фигурой (рис.25). Поэтому указанное условие можно сформулировать так: Для того, чтобы фигура А была квадрируемой, необходимо и достаточно, чтобы Отметим достаточное условие квадрируемости. Теорема 1. Для того, чтобы фигура А была квадрируемой, достаточно, чтобы её граница состояла из конечного числа дуг Гк, являющихся графиками непрерывных функций Доказательство. Покажем сначала, что лугу Г
где
Объединение этих прямоугольников образует ступенчатую фигуру, содержащую дугу Г и имеющую площадь, меньшую, чем Поскольку граница фигуры А состоит из конечного числа таких дуг, её можно накрыть ступенчатой фигурой сколь угодно малой площади, и потому область квадрируема. Например, круг квадрируем, так как его граница состоит из двух дуг, задаваемых уравнениями Иногда оказывается полезным следующее достаточное условие квадрируемости фигур. Теорема 2. Если для любого Доказательство. Зададим
Но тогда
Это и доказывает квадрируемость А. 3. Свойства площадей квадрируемых фигур. Покажем, что площади квадрируемых фигур обладают свойствами, похожими на свойства ступенчатых фигур. Сначала докажем следующее утверждение: а) пусть квадрируемые фигуры А и В не имеют общих внутренних точек и С=А (1) В самом деле, из квадрируемости фигур А и В вытекает, что для любого
(2) Фигуры F2 и G2 могут иметь общие внутренние точки (рис.28), а потому можно утверждать лишь, что (3) Отсюда следует, что
Из неравенств
С другой стороны,
а потому в силу отношений (2) и (3)
Мы видим, что числа
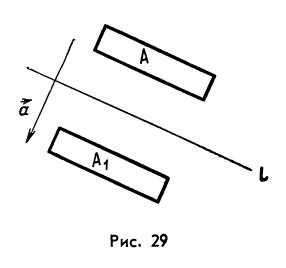
Поэтому указанные множества могут разделяться лишь одним числом. Это и доказывает соотношение (1). Доказанное свойство называют аддитивностью площади. Второе свойство площадей состоит в том, что площадь квадрируемой фигуры не изменяется при параллельном переносе. Это следует из того, что при этом переносе каждая внутренняя ступенчатая фигура для А переходит во внутреннюю ступенчатую фигуру для образа А, и то же самое верно для внешних ступенчатых фигур. Но это значит, что при параллельном переносе не изменяются, ни множество Недостатком данного выше определения площади является то, что оно связано с выбором системы координат на плоскости. Мы доказали лишь, что площадь не изменяется (инвариантна) при параллельных переносах, но не доказали такого же утверждения относительно других перемещений (симметрий, поворотов и т.д.). Справедливо более общее утверждение: б) Если фигура А квадрируема и А1 – конгруэнтная ей фигура, то А1 тоже квадрируема, причём
В курсе геометрии доказывают, что любое перемещение является композицией осевых симметрий. Поэтому достаточно доказать наше утверждение для случая, когда А – прямоугольник, одна из сторон которого параллельна оси симметрии l (рис.29). В этом случае образ А1 этого прямоугольника может быть получен из А не только с помощью осевой симметрии, но и с помощью параллельного переноса. Поэтому Мы доказали, что в классе квадрируемых фигур площадь обладает следующими свойствами: 1°. Для любой фигуры 2°.Площади конгруэнтных фигур равны (инвариантность площади относительно перемещений). 3°.Если фигуры F и G не имеют общих внутренних точек, то
4°.Площадь единичного квадрата равна единице (условие нормировки). Можно доказать, что условия 1°-4° однозначно определяют площадь в классе квадрируемых фигур. Это позволяет понятию площади дать аксиоматическое определение, сказав, что на совокупности фигур М определено понятие площади, если на М задана числовая функция 4. Вычисление площади плоской фигуры в декартовых координатах. Напомним, что мы назвали криволинейной трапецией фигуру, ограниченную осью абсцисс, прямыми х=а и х=b и графиком функции Теорема 3. Если функция (4) Доказательство. Криволинейная трапеция ограничена тремя отрезками и графиком непрерывной функции Тогда, с одной стороны, имеем:
где
Таким образом, числа
Но, как было показано при изучении определённого интеграла, эти множества разделяются лишь одним числом, и потому Теорема доказана.
Аналогично доказывается, что если фигура ограничена снизу графиком функции
Наглядный смысл формулы (4) состоит в том, что криволинейную трапецию можно рассматривать как объединение «бесконечно тонких полосок» с основаниями dx и высотами Пусть теперь функция
Рассмотрим фигуру Ф, симметричную фигуре F относительно оси Ох. Эта фигура (рис.31) представляет собой криволинейную трапецию, ограниченную сверху графиком непрерывной на отрезке [a;b] функции
Но
Как мы видим, в рассматриваемом случае интеграл
Пример 1. Найдём площадь фигуры, ограниченной кривой
Решение. Имеем:
Пример 2. Вычислим площадь фигуры, ограниченной дугой параболы
Решение. Из рисунка видно, что трапеции, площадь которой нужно найти, расположена симметрично относительно оси абсцисс и, следовательно, искомая площадь равна
Пример 3. Найдём площадь, ограниченной графиками функции
Решение. Искомая площадь равна разности площадей криволинейного треугольника ОАВ и прямоугольного треугольника ОАВ:
Пример 4. Вычислим площадь фигуры, ограниченной петлёй кривой
Решение. Из уравнения кривой видно, что она расположена симметрично относительно оси Ох. Следовательно, можно сначала вычислить половину искомой площади (рис.36). Рекомендуем читателю подробно исследовать и построить данную кривую. Записав уравнение кривой в виде Учитывая сказанное, найдём площадь половины петли:
5. Площадь фигуры, ограниченной кривой, заданной параметрическими уравнениями. Пусть кривая
Где функция
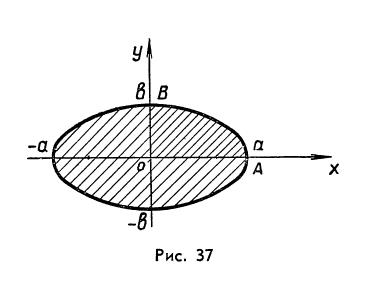
Итак, (5) Пример 5. Вычислим площадь эллипса
Решение. Выберем ту часть эллипса (рис.37), которая расположена в первом квадранте. Точке А(а;0) соответствует значению t=0, а точке В(0;b) – значение
6. Площадь в полярных координатах. Вычислим площадь сектора, ограниченного лучами l и m, выходящими из точки О, и непрерывной кривой Г(рис.38).
Выберем полярную систему координат, полюсом которой является точка О. Пусть
и рассмотрим к -ый частичный сектор
Пусть rk наименьшее значение функции Построим два круговых сектора с радиусами rk и Rk. Обозначим через
Построим аналогичным образом внутренние и внешние круговые секторы для всех частичных криволинейных секторов. Объединяя их, получим внутреннюю и внешнюю фигуры. Площадь внутренней фигуры, состоящей из круговых секторов, равна (6) В тоже время по определению определённого интеграла (7) В силу единственности разделяющего числа из неравенств (6) и (7) следует, что (8) Пример 6. Вычислим площадь, ограниченную одним лепестком кривой
Решение. Значения Поэтому
|


 ,
,  ,...,
,...,  , то говорят, что F разбита на фигуры
, то говорят, что F разбита на фигуры  =ab.
=ab. , то площадь всего прямоугольника равна сумме площадей его частей:
, то площадь всего прямоугольника равна сумме площадей его частей: +
+  .
.
 .
.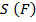 =
=  .
.
 = S (
= S ( + S (
+ S ( .
.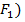 = S (
= S (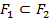 , то
, то  . В самом деле, если присоединить к
. В самом деле, если присоединить к 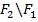 граничные точки, то получится ступенчатая фигура G, не налегающая на
граничные точки, то получится ступенчатая фигура G, не налегающая на 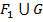 . Значит,
. Значит,  .
. состоит из площадей ступенчатых фигур, все точки которых принадлежат фигуре A, а множество
состоит из площадей ступенчатых фигур, все точки которых принадлежат фигуре A, а множество  - из площадей ступенчатых фигур, содержащих фигуру A. Очевидно, что множество
- из площадей ступенчатых фигур, содержащих фигуру A. Очевидно, что множество 
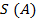 , разделяющее
, разделяющее  нашлись такие ступенчатые фигуры
нашлись такие ступенчатые фигуры 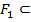 A
A 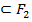 , причем:
, причем: .
. .
.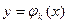 или
или 
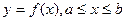 , можно заключить в ступенчатую фигуру, имеющую сколь угодно малую площадь. Зададим
, можно заключить в ступенчатую фигуру, имеющую сколь угодно малую площадь. Зададим 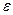 >0. Так как функция
>0. Так как функция  непрерывна на отрезке
непрерывна на отрезке 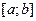 , найдётся разбиение
, найдётся разбиение 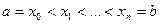 этого отрезка такое, что для любого к выполняется неравенство
этого отрезка такое, что для любого к выполняется неравенство
 и
и  - соответственно наибольшее и наименьшее значения функции
- соответственно наибольшее и наименьшее значения функции  и высоты
и высоты 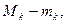 (рис.26). Общая площадь этих прямоугольников не превосходит числа
(рис.26). Общая площадь этих прямоугольников не превосходит числа
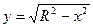 и
и 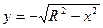 ,
, 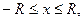 а эти функции непрерывны.
а эти функции непрерывны. найдутся такие квадрируемые фигуры А1 и А2, что
найдутся такие квадрируемые фигуры А1 и А2, что 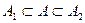 и
и 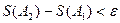 , то фигура А тоже квадрируема.
, то фигура А тоже квадрируема.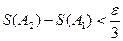 . Так как
. Так как  и
и 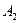 квадрируемы, то найдутся такие ступенчатые фигуры
квадрируемы, то найдутся такие ступенчатые фигуры 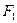 и
и 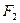 , что
, что  и
и  , причём
, причём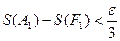 и
и  .
.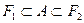 и
и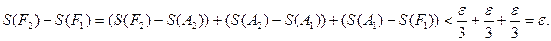
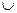 В. Тогда фигура С тоже квадрируема, причём её площадь равна сумме площадей фигур А и В:
В. Тогда фигура С тоже квадрируема, причём её площадь равна сумме площадей фигур А и В: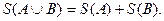
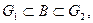 причём
причём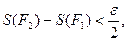
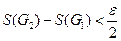 .
. Положим
Положим  b
b 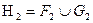 . Тогда Н1 – ступенчатая фигура, содержащаяся в А
. Тогда Н1 – ступенчатая фигура, содержащаяся в А  А
А 
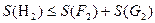
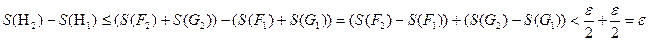 Итак, для любого
Итак, для любого  .
. и
и  вытекает, что
вытекает, что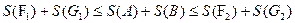 .
.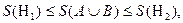
 .
.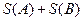 и
и  разделяют одни и те же множества
разделяют одни и те же множества 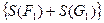 и
и 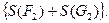 При этом, как было показано, для любого
При этом, как было показано, для любого 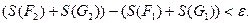
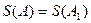 .
.
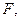 её площадь
её площадь 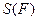 - неотрицательно число (неотрицательность площади).
- неотрицательно число (неотрицательность площади).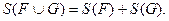 (аддитивность площади).
(аддитивность площади).

 - площадь внутренней ступенчатой фигуры,
- площадь внутренней ступенчатой фигуры,  - площадь внешней ступенчатой фигуры. С другой стороны, по определению интеграла можно записать:
- площадь внешней ступенчатой фигуры. С другой стороны, по определению интеграла можно записать: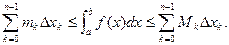
 и
и 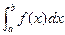 разделяют одни и те же числовые множества:
разделяют одни и те же числовые множества: и
и 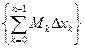 .
.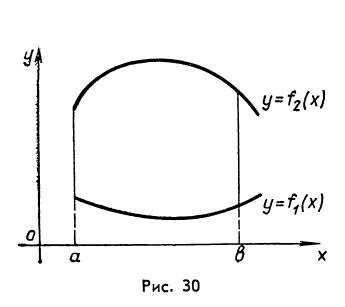
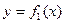 , сверху графиком функции
, сверху графиком функции 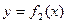 , а слева и справа прямыми
, а слева и справа прямыми 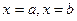 (рис.30), то её площадь выражается формулой:
(рис.30), то её площадь выражается формулой: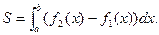
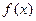 .
.
 , которая на [a;b] принимает только неотрицательные значения. По доказанному выше
, которая на [a;b] принимает только неотрицательные значения. По доказанному выше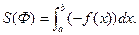
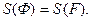 Значит,
Значит, .
.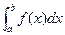 даёт значение площади криволинейной трапеции F с точностью до знака. Если же функция f меняет знак на отрезке [a;b] в конечном числе точек, то значение интеграла
даёт значение площади криволинейной трапеции F с точностью до знака. Если же функция f меняет знак на отрезке [a;b] в конечном числе точек, то значение интеграла 
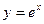 , осью абсцисс и прямыми х=1, х=2. (рис.33).
, осью абсцисс и прямыми х=1, х=2. (рис.33).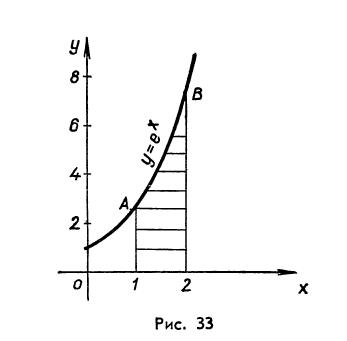
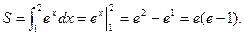
 и отрезком прямой
и отрезком прямой 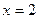 . (рис.34)
. (рис.34)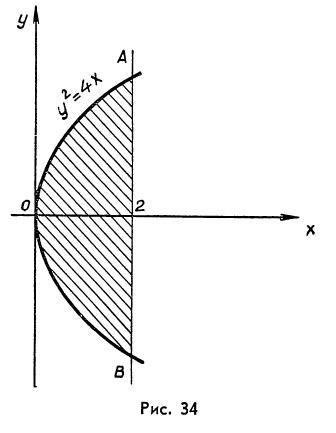
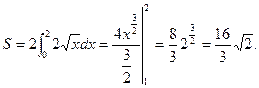
 ,
,  (рис.35).
(рис.35).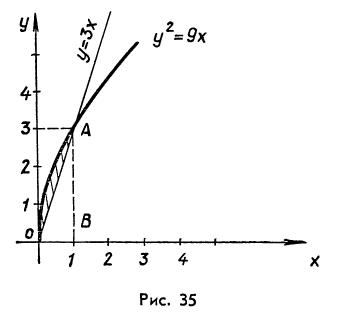



 найдём точки пересечения с осью Ох, положив у=0: х1=0, х2=а.
найдём точки пересечения с осью Ох, положив у=0: х1=0, х2=а.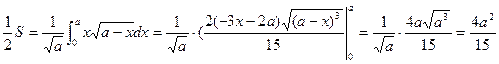 .
.
 , задана в параметрической форме
, задана в параметрической форме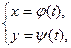

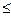 t
t 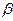 ,
,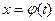 монотонна на отрезке
монотонна на отрезке  , причём
, причём  и имеет на этом отрезке непрерывную производную. Так как
и имеет на этом отрезке непрерывную производную. Так как 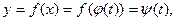 то по формуле замены переменной под знаком определённого интеграла получаем:
то по формуле замены переменной под знаком определённого интеграла получаем: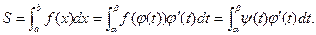
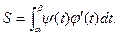


 ,
,
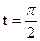 . Поэтому
. Поэтому Итак,
Итак, 
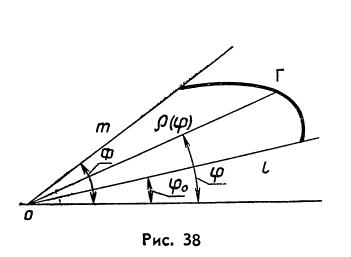
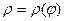 - полярное уравнение кривой Г, а
- полярное уравнение кривой Г, а 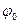 и Ф – углы между полярной осью и лучами l и m соответственно. При этом пусть функция
и Ф – углы между полярной осью и лучами l и m соответственно. При этом пусть функция  непрерывна на
непрерывна на 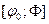 . Разобьём данный сектор на n частей лучами
. Разобьём данный сектор на n частей лучами
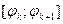 (рис.39).
(рис.39).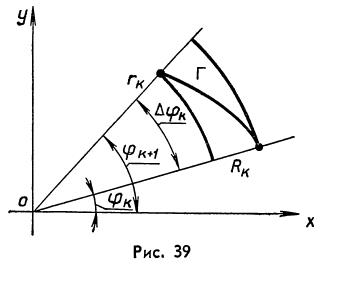
 величину угла рассматриваемого частичного сектора. Тогда площадь частичного криволинейного сектора будет заключена между площадями вписанного и описанного частичных круговых секторов
величину угла рассматриваемого частичного сектора. Тогда площадь частичного криволинейного сектора будет заключена между площадями вписанного и описанного частичных круговых секторов
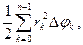 а площадь верхней фигуры равна
а площадь верхней фигуры равна 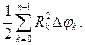 Эти выражения являются нижней и верхней суммами Дарбу sp и Sp для интеграла
Эти выражения являются нижней и верхней суммами Дарбу sp и Sp для интеграла  . Так как функция
. Так как функция 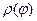 непрерывна, то непрерывна, а потому и интегрируема, функция
непрерывна, то непрерывна, а потому и интегрируема, функция  . Поэтому для любого
. Поэтому для любого 
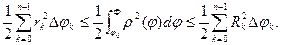

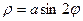 (рис.40).
(рис.40).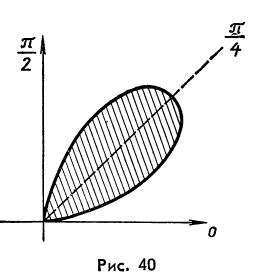
 и
и  соответствуют
соответствуют 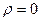 .
.



