Вывод формулы длины дуги регулярной кривой.
Лемма. Пусть жорданова кривая регулярна и l (t) – длина дуги этой кривой, ограниченной точками М(а) и М(b). Тогда функция l (t) дифференцируема на отрезке[ a;b ], причём для всех t имеем: (8) Доказательство. Возьмём любое t
Перейдём к пределу при
и
а потому
Лемма доказана. Из этой леммы следует, что (9) Так как
Геометрический смысл этой формулы ясен из рисунка 50, где Теорема 2. Если жорданова кривая Г:
Регулярна, то его длина выражается формулой (10) Доказательство. Так как l=l(a)-l(b)= Теорема доказана. Полученную формулу можно переписать в следующих видах: (10') (10'') (10''') Пример 1. Рассмотрим длину дуги астроиды Решение. Данная кривая симметрична относительно обеих координатных осей, поэтому достаточно найти длину четверти дуги, расположенной в первом квадранте ( Найдём производные: Вычислим сумму: Учитывая сказанное выше, найдём четверть длины астроиды:
Длина всей кривой 4. Частные случаи формулы длины кривой. Рассмотрим частные случаи общей формулы (10) п.3. Если кривая Г задана явным уравнением
(11) Полученную формулу записывают короче в виде (11') Значит, (12) Пример 2. Вычислим длину дуги цепной линии
Найдём производную
Вычислим подкоренное выражение
Длина l указанного отрезка цепной линии будет
Рассмотрим теперь случай, когда кривая Г задана в полярных координатах уравнением Так как декартовы координаты связаны с полярными координатами точек плоскости соотношениями
отсюда находим:
Поэтому
В силу формулы (10) п.3 имеем: (13) Пример 3. Вычислим длину кардиоиды Решение. Данная функция
Поэтому сначала найдём половину длины дуги данной кривой, для которой полярный угол
Из формулы (13) получаем выражение дли дифферинциала дуги, заданной полярным уравнение (14)
Геометрическую иллюстрацию даёт рисунок 53. На этом рисунке АС – дуга рассматриваемой кривой, АВ – дуга окружности с центром в точке О и радиусом
5. Необходимое и достаточное условие спрямляемости кривой. Данное в п.2 условие спрямляемости кривой является достаточным, но не необходимым (например, любая ломаная спрямляема, но не регулярна, так как имеет точки излома).Чтобы сформулировать необходимое и достаточное условие спрямляемости кривой, нам понадобится понятие: функция с ограниченным изменением. Рассмотрим функцию y=f(x), определённую на отрезке [ a;b ], и произвольное разбиение Р этого отрезка:
Для каждого частичного промежутка
Полученная сумма называется изменением функции Рассмотрим множество
Теперь мы можем сформулировать и доказать необходимое и достаточное условие спрямляемости жордановой кривой. Теорема 3. Для того чтобы жорданова кривая Г:
была спрямляемой, необходимо и достаточно, чтобы непрерывные функции Доказательство. Покажем сначала, что ограниченность изменения функции
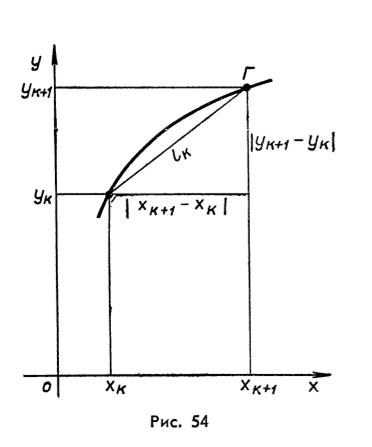
Но из рисунка 54 видно, что Эти неравенства можно переписать следующим образом:
и
Они показывают, что для любого разбиения Р отрезка Теперь докажем, что если функции
и
Иными словами,
и
Но из рисунка 54 видно, что
Поэтому для любой ломаной
и потому кривая Г спрямляема.
|

 .
.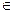 [a;b] и дадим t приращение
[a;b] и дадим t приращение 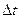 такое, что t +
такое, что t + 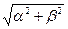
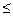
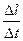
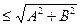 .
. 0. В силу непрерывности функций
0. В силу непрерывности функций 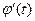 и
и 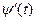 в точке t получаем, что
в точке t получаем, что
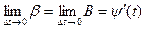 ,
,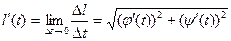 .
.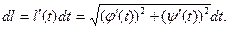
 ,
,  , то формулу (9) можно переписать в виде
, то формулу (9) можно переписать в виде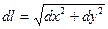 .
.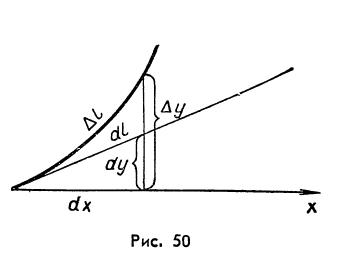
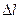 - участок дуги, а
- участок дуги, а 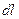 - соответствующий отрезок касательной. Мы будем называть
- соответствующий отрезок касательной. Мы будем называть 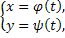
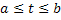 ,
,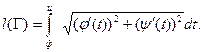
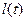 - первообразная для
- первообразная для 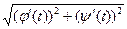 , а тогда
, а тогда 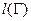 равна разности значений первообразной, т.е.
равна разности значений первообразной, т.е.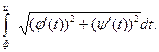
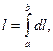
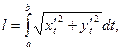
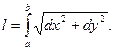
 ,
, 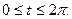
 )
)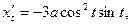

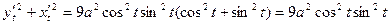
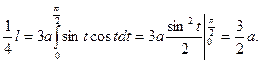
 . Она мало отличается от
. Она мало отличается от 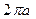 , т.е. от длины окружности, описанной вокруг астроиды.
, т.е. от длины окружности, описанной вокруг астроиды.
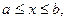 то её можно представить параметрическими уравнениями
то её можно представить параметрическими уравнениями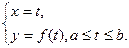
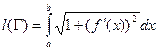 .
.
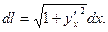
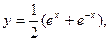 взятой от точки х=0 до точки х=1 (рис.51).
взятой от точки х=0 до точки х=1 (рис.51).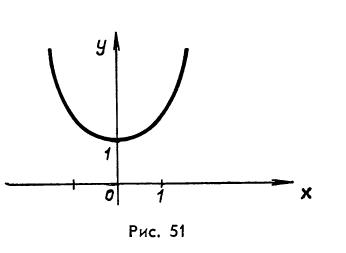
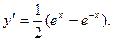
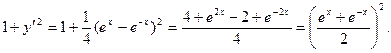
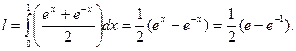
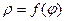 , где
, где 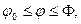 причём функция
причём функция  на отрезке [
на отрезке [ 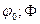 ] имеет непрерывную производную
] имеет непрерывную производную 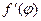 .
.
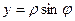 , полярное уравнение данной кривой можно записать в виде параметрических уравнений:
, полярное уравнение данной кривой можно записать в виде параметрических уравнений: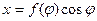 ,
, 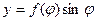 ;
;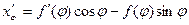 ,
, 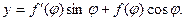
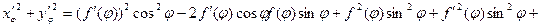
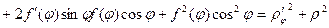 .
.
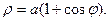
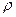 чётная, следовательно, кривая расположена симметрично относительно полярной оси (рис.52).
чётная, следовательно, кривая расположена симметрично относительно полярной оси (рис.52).
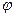 изменяется от 0 до 2
изменяется от 0 до 2 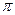 , после чего удвоим полученный результат:
, после чего удвоим полученный результат: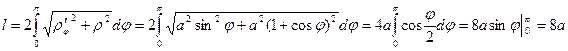 .
.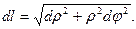

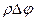 - длина дуги АВ. Заменяя
- длина дуги АВ. Заменяя 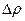 и
и 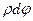 ,
,  и
и 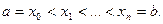
 разбиения Р образуем разность
разбиения Р образуем разность  - приращение функции на этом промежутке. Эта разность может быть как положительной, так и отрицательной. Заменим все эти разности их модулями и сложим. Получим сумму
- приращение функции на этом промежутке. Эта разность может быть как положительной, так и отрицательной. Заменим все эти разности их модулями и сложим. Получим сумму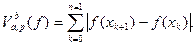
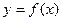 , соответствующим разбиению Р отрезка
, соответствующим разбиению Р отрезка 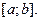
 изменений функции
изменений функции 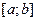 , а точную верхнюю границу этого множества называют изменением функции
, а точную верхнюю границу этого множества называют изменением функции 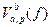 . Таким образом,
. Таким образом,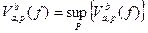 .
. a
a 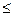 t
t 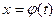 и
и 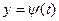 имели ограниченное изменение на отрезке
имели ограниченное изменение на отрезке 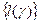 длин вписанных в неё ломанных ограничено сверху некоторым числом М. Это означает, что для любой вписанной в Г ломанной имеем:
длин вписанных в неё ломанных ограничено сверху некоторым числом М. Это означает, что для любой вписанной в Г ломанной имеем: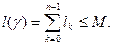
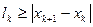 и
и 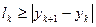 , а потому
, а потому 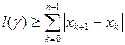 и
и 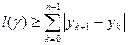 .
.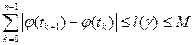
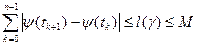 .
.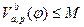 и
и 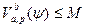 , т.е. функции
, т.е. функции 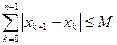
 .
.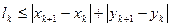 .
. , вписанной в кривую Г, имеем:
, вписанной в кривую Г, имеем: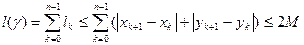 ,
,


