Вычисление объёмов тел.
1.Кубируемые тела. В этом параграфе рассмотрим вопрос о вычислении объёмов тел. Начнём с простейших тел – прямоугольных параллелепипедов. Выберем в пространстве прямоугольную декартовую систему координат O xyz. Пусть А – допустимый прямоугольный параллелепипед (параллелепипед, стороны которого параллельны осям координат), длины рёбер которого равны а, в, с. Назовём число а в с объёмом этого параллелепипеда и обозначим его V(А), V(А) = а в с. Очевидно, что если параллелепипед А разделён плоскостью, параллельной одной из координатных плоскостей, на параллелепипеды В и С, то выполняется равенство V(А) = V(В) + V(С). Далее, если параллелепипед А' получается из параллелепипеда А параллельным переносом, то V(А') = V(А). Наконец, объём куба с длиной ребра 1 равен 1. Мы хотим распространить понятие объёма на более широкий класс тел, чем класс допустимых параллелепипедов. Назовём ступенчатым любое тело L, которое можно представить в виде объединения конечного числа таких параллелепипедов, никакие два из которых не имеют общих внутренних точек. Пусть L = V(L) = Это определение не зависит от того, каким способом тело L разложено на параллелепипеды. Возьмём теперь любое тело Т. Обозначим через ХТ числовое множество, состоящее из объёмов ступенчатых тел, целиком содержащихся в Т, а через УТ – множество объёмов ступенчатых тел, содержащих Т: ХТ = { V внутренних ступенчатых тел }, УТ = { V внешних ступенчатых тел }. Тогда числовое множество ХТ лежит левее числового множества УТ. В самом деле, если х Поскольку ХТ лежит левее УТ, то найдётся хотя бы одно число, разделяющее эти множества. Если ХТ и УТ разделяются лишь одним числом, то тело Т называют кубируемым, а число, разделяющее множества ХТ и УТ – объёмом этого тела. Его обозначают V(Т). Итак, объёмом кубируемого тела называют единственное число, разделяющее множество ступенчатых тел, содержащихся в Т, и множество объёмов ступенчатых тел, содержащих Т. Применяя необходимое и достаточное условие единственности разделяющего числа, получим следующее необходимое и достаточное условие кубируемости тела: Для того, чтобы тело т было кубируемым, необходимо и достаточно, чтобы для любого Объём тел обладает свойством аддитивности: Если Т1 и Т2 – кубируемые тела, не имеющие общих внутренних точек, то их объединение Т = Т1 V(Т) = V(Т1) + V(Т2). Мы опускаем доказательство этого утверждения, поскольку оно проводится так же, как и для площадей. Отметим только, что внутренней точкой тела Т называется всякая точка, которая принадлежит телу Т вместе с некоторой своей окрестностью (т.е. открытым шаром с центром данной точке). Далее очевидно, что если тело Т кубируемо, а тело Т1 получается из Т параллельным переносом, то тело Т1 также кубируемо, причём V(Т) = V(Т1). Можно доказать, что справедливо более общее утверждение: если тело Т1 конгруэнтно кубируемому телу Т, то Т1 кубируемо и V(Т) = V(Т1). Понятие объёма можно определить и аксиоматически теми же требованиями 1°–4°, что и площадь. Разница состоит лишь в том, что иначе понимается условие отсутствия общих внутренних точек (окрестности берутся не на плоскости, а в пространстве) и иначе выглядит условия нормировки. Мы будем использовать в дальнейшем достаточное условие кубируемости тела. Если для любого
|

 Fj – разложение ступенчатого тела на такие параллелепипеды. Положим по определению, что
Fj – разложение ступенчатого тела на такие параллелепипеды. Положим по определению, что V (Fj).
V (Fj). ХТ и у
ХТ и у  Т
Т 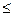 V(L2), а это и значит, что х
V(L2), а это и значит, что х 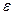 > 0 нашлись ступенчатые тела L1 и L2 такие, что L1
> 0 нашлись ступенчатые тела L1 и L2 такие, что L1 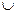 Т2 также кубируемо, причём выполняется равенство
Т2 также кубируемо, причём выполняется равенство


