Вычисление объёма тела по площадям параллельных сечений.
В этом пункте мы выведем основную формулу, позволяющую выразить объём тела через площади сечений этого тела, параллельных некоторой плоскости. Определение. Тело Т назовём регулярным, если существует такая плоскость П, что а) тело Т лежит по одну сторону от этой плоскости; б) все сечения тела Т плоскостями, параллельными плоскости П, квадрируемы; в) площадь S (x) сечения Q (x), параллельного плоскости П и отстоящего от неё на расстояние х, является непрерывной функцией от х; г) если S (х1) и S (х2), то проекция сечения Q (x2) на плоскость П содержит проекцию сечения Q (x1) на ту же плоскость. Теорема 2. Если тело Т регулярно, то оно кубируемо, причём его объём выражается формулой (2) V (T) = Здесь S (x) – площадь сечения тела т плоскостью, параллельной плоскости П и отстоящей от неё на расстояние х, а – наименьшее из расстояний точек тела Т от плоскости П, в – наибольшее из этих расстояний (см. рис. 42, где а = 0).
Доказательство. Рассмотрим некоторое разбиение отрезка [ а; в ]: а = х 0 < х 1 < х 2 < … < х n < = b и на расстояниях х 0, х 1, х 2 , …, х n проведём плоскости, параллельные плоскости П. Данное тело Т этими плоскостями разобьётся на частичные «ломтики» Т0, Т1, …, Тn-1. Рассмотрим к -ый частичный «ломтик». Его высота равна Vк = s к Объём Vк внешнего цилиндрического тела будет Vк = S к Объединяя все внутренние и все внешние цилиндрические тела, получим два тела L1 и L2 такие, что L1
а объём тела L2 равен
Но
т.е. V (L2) - V (L1) < Отсюда следует, что тело Т кубируемо. При этом объём тела V (T) удовлетворяет неравенствам
Но с другой стороны,
Значит, числа V (T) и { Поскольку эти множества разделяются лишь одним числом, то V (T) = Пример 1. Вычислить объём пирамиды, площадь основания которой равна S, а высота H (рис.43).
Решение. Так как Следовательно, V = Пример 2. Вычислим объём шарового слоя, отсеченного от шара х 2 + у 2 + z 2 = 9 плоскостями х = 1 и х = 2. Решение. Плоскость, перпендикулярная к оси абсцисс в точке х, пересекает шар по кругу радиуса r = и, следовательно V = 4. Принцип Кавальери. Из формулы (2) п.3 вытекает следующее утверждение, называемое принципом Кавальери.
Доказательство. Обозначим через V1 объём тела Т1, а через V2 – объём тела Т2. Так как тела Т1 и Т2 кубируемы, то V1 (T1) = По условию, S1 (x) = S2 (x), значит, и V1 = V2. Пример 3. Покажем, что объём полушара радиуса R равен разности объёмов цилиндра, радиус основания и высота которого равны R, и конуса с радиусом основания R (рис.45).
Обозначим через S2 (x) площадь сечения тела (цилиндр без конуса) плоскостью, параллельной основанию цилиндра и отстоящей от него на расстоянии х: S2 (х) = Из подобия треугольников ОАВ и ОСD имеем: 5. Объём тела вращения. Пусть Т – тело вращения, образованное вращение вокруг оси абсцисс криволинейной трапеции, расположенной в верхней полуплоскости и ограниченной осью абсцисс, прямыми х = а, х = в и графиком непрерывной функции у = f (x). Докажем, что это тело вращения кубируемо и его объём выражается формулой (3) V = Сначала докажем, что это тело вращения регулярно, если в качестве П выберем плоскость О уz, перпендикулярную оси вращения. Отметим, что сечение, находящееся на расстоянии х от плоскости О уz, является кругом радиуса f (x) и его площадь S (х) равна
Поэтому функция S (х) непрерывна в силу непрерывности f (x). Далее, если S (х1) Итак, тело вращения регулярно. Следовательно, оно кубируемо и его объём вычисляется по формуле V = Если бы криволинейная трапеция была ограничена и снизу и сверху кривыми у1 = f (x1) и у2 = f (x2), то V = Формулой (3) можно воспользоваться и для вычисления объёма тела вращения в случае и для вычисления объёма тела вращения в случае, когда граница вращающейся фигуры задана параметрическими уравнениями. В этом случае приходится пользоваться заменой переменной под знаком определённого интеграла. В некоторых случаях оказывается удобным разлагать тела вращения не на прямые круговые цилиндры, а на фигуры иного вида. Например, найдём объём тела, получаемого при вращении криволинейной трапеции вокруг оси ординат. Сначала найдём объём, получаемый при вращении прямоугольника с высотой ук , в основании которого лежит отрезок [ хк; хк+1 ]. Этот объём равен разности объёмов двух прямых круговых цилиндров
Но теперь ясно, что искомый объём оценивается сверху и снизу следующим образом:
Отсюда легко следует, что (4) V = 2 Пример 4. Найти объём шара радиуса R. Решение. Не теряя общности, будем рассматривать круг радиуса R с центром в начале координат. Этот круг, вращаясь вокруг оси О х, образует шар. Уравнение окружности имеет вид х 2 + у 2 = R, поэтому у 2 = R - х 2. Учитывая симметрию круга относительно оси ординат, найдём сначала половину искомого объёма
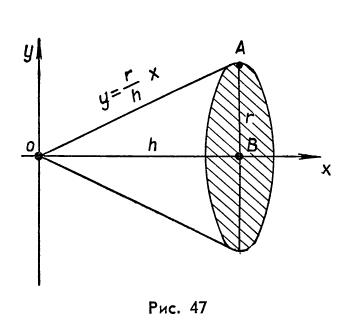
Пример 5. вычислим объём конуса, высота которого h и радиус основания r.
Решение. Выберем систему координат так, чтобы ось О х совпала с высотой h (рис.47), а вершину конуса примем за начало координат. Тогда уравнение прямой ОА запишется в виде у = Пользуясь формулой (3), получим: V = Пример 6. Найдём объём тела, полученного при вращении вокруг оси абсцисс астроиды х = a cos3t, y = a sin3t. (рис.48).
Решение. Построим астроиду. Рассмотрим половину верхней части астроиды, расположенной симметрично относительно оси ординат. Используя формулу (3) и меняя переменную под знаком определённого интеграла, найдём для новой переменной t пределы интегрирования. Если х = a cos3t = 0, то t = Учитывая, что y2 = a2 sin6t, dx = - 3a cos2t sint dt, получаем: V = Применяя реккурентную формулу, получаем, что V = 3 Объём всего тела вращения будет Пример 7. Найдём объём тела, получаемого при вращении вокруг оси ординат криволинейной трапеции, ограниченной осью абсцисс и первой аркой циклоиды x = a (t – sint), y = a(1 – cost). Решение. Воспользуемся формулой (4): V = 2 И заменим переменную под знаком интеграла, учитывая, что первая арка циклоиды образуется при изменении переменной t от 0 до 2 V = 2
|

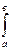 S (x) dx.
S (x) dx.
 хк = хк+1 – хк. Так как функция у = S (x) непрерывна на [ хк; хк+1 ], то она принимает на этом отрезке наибольшее и наименьшее значения. Наименьшее значение площади сечения для этого «ломтика» обозначим s к и S к. В силу условия г) регулярности тела Т цилиндрическое тело с основанием s к лежит внутри частичного «ломтика», а цилиндрическое тело с основанием S к целиком его содержит. Объём Vк внутреннего цилиндрического тела будет
хк = хк+1 – хк. Так как функция у = S (x) непрерывна на [ хк; хк+1 ], то она принимает на этом отрезке наибольшее и наименьшее значения. Наименьшее значение площади сечения для этого «ломтика» обозначим s к и S к. В силу условия г) регулярности тела Т цилиндрическое тело с основанием s к лежит внутри частичного «ломтика», а цилиндрическое тело с основанием S к целиком его содержит. Объём Vк внутреннего цилиндрического тела будет L
L 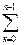 s к
s к 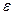 > 0 найдётся такое разбиение отрезка [ а; в ], что
> 0 найдётся такое разбиение отрезка [ а; в ], что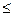 V (T)
V (T) 
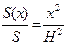 , то S(x) =
, то S(x) = 
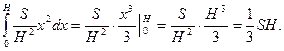
 . Площадь сечения S (х) =
. Площадь сечения S (х) = 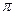 r2 =
r2 = 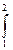 (9 - х 2 ) dx =
(9 - х 2 ) dx = 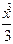 )
) 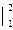 = 6
= 6 
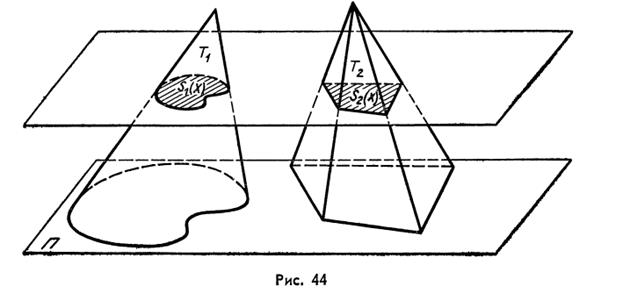 Два кубируемых тела Т1 и Т2 (рис.44), ограниченные параллельными плоскостями, имеют равнее объёмы, если плоские сечения, параллельные указанным плоскостям и проведённые на одинаковых расстояниях от оснований, имеют равные площади.
Два кубируемых тела Т1 и Т2 (рис.44), ограниченные параллельными плоскостями, имеют равнее объёмы, если плоские сечения, параллельные указанным плоскостям и проведённые на одинаковых расстояниях от оснований, имеют равные площади. Рассмотрим полушар. Обозначим через S1 (x) площадь сечения, параллельного плоскости основания полушара, отстоящего от него на расстоянии х. Учитывая, что r2= R 2 – х 2, найдём S1 (х) =
Рассмотрим полушар. Обозначим через S1 (x) площадь сечения, параллельного плоскости основания полушара, отстоящего от него на расстоянии х. Учитывая, что r2= R 2 – х 2, найдём S1 (х) = 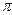 R 2 -
R 2 - 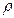 2 =
2 =  =
= 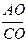 или
или  =
=  , откуда
, откуда  f 2 (x) dx =
f 2 (x) dx = 
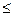 S (х2), то значит, что f (х1)
S (х2), то значит, что f (х1) 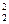 dx –
dx –  dx =
dx =  Vk =
Vk = 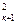 –
– 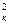 =
= 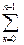 m к x k
m к x k  Vш =
Vш =  у2 dх =
у2 dх = 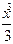 )
) 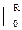 =
= 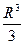 ) =
) = 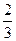
 .
.

 , а если х = a cos3t = а, то t = 0.
, а если х = a cos3t = а, то t = 0.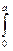 у2 dх =
у2 dх = 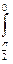 ( – 3a cos2t sint) a2 sin6t dt = 3
( – 3a cos2t sint) a2 sin6t dt = 3  sin6t cos2t sint dt = 3
sin6t cos2t sint dt = 3  ) = 3
) = 3  (9 – 8) = 3
(9 – 8) = 3  =
= 

 a (t – sint) a (1– cost) a (1– cost) dt = 2
a (t – sint) a (1– cost) a (1– cost) dt = 2 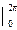 = 2
= 2 


