Объём прямого цилиндрического тела.
Пусть F – плоская фигура. Восставим в каждой точке этой фигуры перпендикуляр к содержащей её плоскости и отложим на каждом перпендикуляре отрезок длины h (все отрезки располагаются по одну сторону от плоскости). Множество точек этих отрезков образует тело L, которое называется прямым цилиндрическим телом с основание F и высотой h. Вторые концы построенных отрезков образуют фигуру F', конгруэнтную основанию F и параллельные ему. В случае, когда F – прямоугольник, прямое цилиндрическое тело является прямоугольным параллелепипедом. Если же F – ступенчатая фигура, то L – ступенчатое тело, причём оно разлагается на прямоугольные параллелепипеды, имеющие одинаковые высоты. Объём этого ступенчатого тела равен произведению площади фигуры F на высоту тела: (1) V (L)=S (F) h. Докажем, что формула (1) остаётся справедливой и в более общем случае. Именно, справедливо следующее утверждение: Теорема 1: Если плоская фигура А квадрируема, то прямое цилиндрическое тело L с основание А кубируемо, причём его объём равен произведению площади фигуры А на высоту тела: V (L) = S (А) h. Доказательство: Не теряя общности, мы можем считать, что плоскость фигуры А является координатной плоскостью Оху. Так как по условию фигура А квадрируема, то для любого Построим ступенчатые тела L1 и L2 с высотой h и основаниями F1 и F2. Тогда имеем: L1 При этом V (L2) - V (L1) = S (F2) h – S (F1) h = h (S (F2) – S (F1)) < h Таким образом, для любого L1 Поэтому тело L кубируемо. При этом, как мы видели, S (F1) h < V (L) < S (F2) h. С другой стороны, из неравенств S (F1) < S (А) < S (F2) вытекает, что S (F1) h < S (А) h < S (F2) h. Мы видим, что числа V (L) и S (А) h разделяют одни и те же множества, а именно { S (F1) h } и { S (F2) h }, где, напомним, F1 – ступенчатые фигуры, содержащиеся в А, а F2 – ступенчатые фигуры, содержащие А. Но эти два множества, в силу квадрируемости А, разделяются лишь одним числом. Поэтому V (L) = S (А) h. Формула (1) доказана для любых квадрируемых фигур А.
|

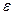 > 0 найдутся ступенчатые фигуры F1 и F2 такие, что F1
> 0 найдутся ступенчатые фигуры F1 и F2 такие, что F1  А
А 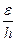 .
.


