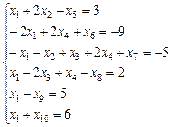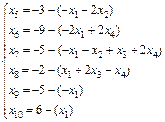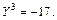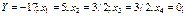Решение частично целочисленной задачиМаксимизировать целевую функцию вида:
При ограничениях:
a) Метод Гомори для частично целочисленных задач. Решаем исходную задачу линейного программирования. Ее решение приведено в пункте 1.3. Последняя симплексная таблица имеет вид:
Значения целевой функции и переменных: Значение переменной В соответствии с правилами формирования коэффициентов ограничений метода Гомери для частично целочисленных задач имеем: Вводим дополнительную свободную переменную: Выражаем новое ограничение в форме Куна-Таккера: Решаем новую расширенную задачу линейного программирования:
Полученное оптимальное решение удовлетворяет поставленным ограничением и требованию целочисленности переменной Ответ:
б) Метод ветвей и границ. Проанализировав ограничения определим границы
Т.к. о целевой функции ничего не известно, примем Решаем Задачу 1 – исходную задачу линейного программирования. Ее решение приведено в пункте 1.3. Последняя симплексная таблица имеет вид:
Значения целевой функции и переменных: Принимаем Полученное решение не удовлетворяет требованиям целочисленности для переменной Поэтому составляем относительно первой задачи две новых порожденных задачи: Задача 2. Максимизировать целевую функцию вида:
При ограничениях:
Преобразуем новую систему ограничений Задачи 2, введя свободные переменные и приведя их к форме Куна-Таккера:
Воспользуемся симплекс методом и решим Задачу 2.
Допустимого решения Задачи 2 не существует. Поэтому примем Выбираем и решаем Задачу 3. Максимизировать целевую функцию вида:
При ограничениях:
Преобразуем новую систему ограничений Задачи 3, введя свободные переменные и приведя их к форме Куна-Таккера:
Воспользуемся симплекс методом и решим Задачу 2.
Полученное оптимальное решение удовлетворяет поставленным ограничением и требованию целочисленности переменной Т.к. список задач, подлежащих решению пуст, то можно сделать вывод о том, что решение задачи целочисленного программирования завершено. Ответ:
Рис 2.2.1 Блок схема решения.
На основе полученных результатов решения задачи методом Гомори и методом ветвей и границ, можно сделать вывод о том, метод Гомори менее трудоемок. Однако, стоит учесть простоту решаемой задачи, в которой требование целочисленности наложено всего на одну переменную из трех. Метод Гомори в данном случае позволяет получить оптимальное решение с использованием всего одного уравнения отсекающей плоскости и решением одной расширенной задачи. Используя метод ветвей и границ, приходится решать уже две порожденных задачи, т.е. использование этого метода в данном случае менее эффективно. Таким образом можно сделать вывод о том, что метод ветвей и границ вообще мало эффективен для решения простых задач, где не требуется получение всех локальных оптимумов. В таких случаях разумнее воспользоваться методом Гомори для частично целочисленных задач.
|
; 
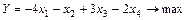
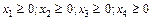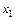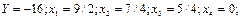
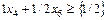
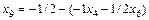
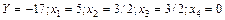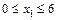
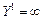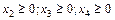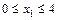- целoе.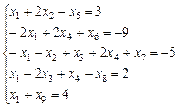
.
.
;
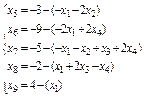
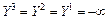
- новое ограничение.
- новое ограничение.
