Решение задачи методом отсекающих плоскостейМаксимизировать целевую функцию
При ограничениях:
Для решения этой полностью целочисленной задачи воспользуемся методом Гомори. Решаем исходную задачу линейного программирования. Ее решение приведено в пункте 1.3. Последняя симплексная таблица имеет вид:
Значения целевой функции и переменных: На основе этой симплексной таблицы для базисной переменной
Вводим новую свободную переменную: Выражаем новое ограничение в форме Куна-Таккера: Добавляем это ограничение к условиям оптимального решения и решаем новую расширенную задачу симплекс методом.
Требование целочисленности не выполнено. Составляем следующее уравнение отсекающей плоскости. Т.к. дробные части у всех нецелых значений базисных переменных равны, выберем любую, например Аналогично:
Теперь решаем новую расширенную задачу.
Полученное оптимальное решение удовлетворяет поставленным ограничениям и требованиям целочисленности. Ответ:
|
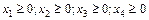и целые.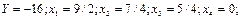
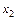, у которой наибольшая дробная часть, строим уравнение отсекающей плоскости.
.
.
.
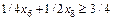
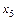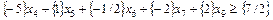
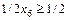
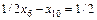
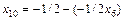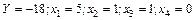