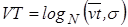Значение Времени как logN-распределенная случайная величина
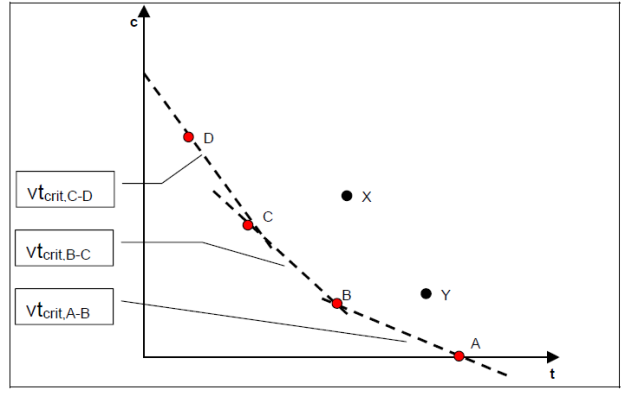
Как упомянуто прежде, предполагается, что каждый пользователь применяет свое индивидуальное значение времени VT. Это предположение отражено в модели, и определяет значение времени VT как случайную величину с распределением логарифмически нормального типа:
Со следующими параметрами распределения:
s – стандартное отклонение добавленной случайной величины Y=loge (VT), где Y нормально распределяется.
• logN-распределение широко используется в статистике дохода. Одно важное свойство logN-распределения для моделирования дохода или дорожных потерь в том, что вероятность равняется нулю для отрицательных значений, которые являются тривиальным предположением для значений времени. • использование медианы . Однако logN-распределение могло быть также определено скупым средним (предполагаемым) μ =loge (vt) и стандартным отклонением σ обоих из присоединенных нормальных распределений Y=loge (VT). Плотность g(vt) и функция распределения
Иллюстрация 2: Функция плотности
Иллюстрация 3:Функция распределения Использование TRIBUT в проектах планирования для формирования распределения VT, то есть этих двух параметров, является одним из самых решающих шагов. Поэтому эмпирические методы настройки (определения) параметров распределения обсуждены (спорны). 2.4.8.3 Поиск Пути: Эффективная Граница как Исключительный Критерий В методах монокритерия один единственный лучший путь (самый короткий путь) может быть определен для каждой OD пары. В случае TRIBUT, однако, из-за случайного распределения VT, многочисленные “лучшие пути” должны быть определены и сохранены в памяти данных не только во время поиска пути, но и во время всего технологического процесса назначения. Это - причина для высокой степени интеграции методов мультикритерия. Однако, возможно сократить эту степень интеграции, идентифицируя эффективные пути для каждой OD пары. Иллюстрация 54 показывает поиск пути с шестью путями, где пути A, B, C и D представляют множество эффективных путей. Легко может быть продемонстрировано или графически или аналитически, что нет никакого VT, для которого пути X или Y были бы предпочтительнее, чем A, B, C или D. Вообще говоря, выпуклая кривая, сформированная тремя критическими VT -прямыми (A-B, B-C и C-D), ограничивает диапазон соответствующих «время-стоимость» комбинаций к правой стороне. Поэтому эту выпуклую кривую называют эффективной границей. Таким образом, X и Y могут быть удалены в примере.
Иллюстрация 4: Критическое значение времени, построенное по направлению к эффективной границе
Введение понятия эффективной границы есть важные следствия: • Только эффективные пути должны быть сохранены во время поиска пути, для последующего выбора пути. Как следствие от большой части различных возможных путей для одной OD пары можно отказаться, ограничивая, таким образом, вычислительное время и память. • Однако TRIBUT должен выполнить одновременный многопутевой поиск, который является более сложным (комплексным), чем технологические процессы поиска лучшего пути в случае монокритерия. • множество эффективных путей для любой OD пары, является единственным для одного состояния сети, не зависит от вида VT -распределения, которое было определено. Следовательно, в случае назначения мультикласса, только один шаг поиска должен быть выполнен на каждой итерации равновесного состояния, хотя последующее распределение спроса будет определяться специально для каждого класса. Алгоритм TRIBUT "многопутевого" поиска состоит из двух шагов: • Сначала, используется классический поиск самого короткого пути с определенным минимальным временем движения от одного начала (координат) 0 ко всем элементам сети. Отметим, что классический самый короткий поиск пути только «утолстил» бы пути от одного пункта отправления до всего предназначения. Этот первый шаг не достаточен, чтобы определить всю эффективную границу, но он найдет самые быстрые пути, которые определенно будут самыми дорогими путями на эффективной границе. • Затем, технологический процесс расширяет дерево путей, дополняя его менее дорогими путями. Это расширение достигнуто тем, что рассматривается не время движения, а критическое значение времени между последним установленным путем объекта сети и другими кандидатами (возможными путями?).
|


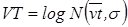
 – медиана (середина?) из
– медиана (середина?) из