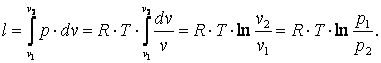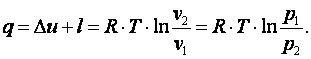Термодинамические процессы: изохорный, изобарный, изотермический, адиабатный, политропный

 

4.2.1.Изохорный процесс (v=const)

Такой процесс может совершаться рабочим телом, находящимся в цилиндре при неподвижном поршне, если к рабочему телу подводится теплота от источника теплоты (см. рис. 4.1) или отводится теплота от рабочего тела к холодильнику. При изохорном процессе выполняется условие dv=0 или v=const. Уравнение изохорного процесса получим из уравнения состояния идеального газа (см. &1.6) при v=const. В pv -координатах график процесса представляет собой прямую линию, параллельную оси p. Изохорный процесс может протекать с повышением давления (процесс 1-2) и с понижением (процесс 1-2’).

Рис. 4.1. График изохорного процесса в p-v координатах

Запишем для точек 1 и 2 уравнения состояния: p₁·v=R·T₁; p₂·v=R·T₂. Следовательно, для изохорного процесса

(4.6)

 

Приращение внутренней энергии газа

(4.7)

 

Работа газа

 

так как dv=0.

Энтальпия газа i_v=u+p·v, а di_v=du+d(p·v)=du+p·dv+v·dp=du+v·dp. Поэтому

(4.8)

 

Энтропия

То есть

(4.9)

4.2.2.Изобарный процесс (p=const)

В p-v координатах график процесса представляет собой прямую линию параллельную оси v (рис. 4.2). Изобарный процесс может протекать с увеличением объёма (процесс 1-2) и с уменьшением (процесс 1-2’). Запишем для точек 1 и 2 уравнения состояния: p·v₁=R·T₁; p·v₂=R·T₂.

Рис. 4.2. График изобарного процессав p-v координатах

Следовательно, для изобарного процесса

(4.10)

 

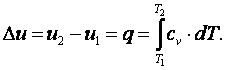
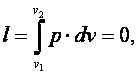
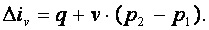
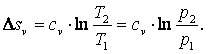
Приращение внутренней энергии газа Работа газа 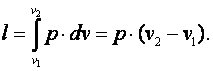Так как p·v₂=R·T₂, а p·v₁=R·T₁, то l=R·(T₂-T₁). Следовательно, газовая постоянная имеет определённый физический смысл: это работа 1 кг газа в изобарном процессе при изменении температуры на один градус. Из выражения (4.3) следует, что в изобарном процессе q=c_p·(T₂-T₁). В соответствии с первым законом термодинамики для изобарного процесса можно записать dq=du+p·dv= du+d(p·v)=di. Поэтому в изобарном процессе di=q=c_p·(T₂-T₁). Из соотношений, характеризующих изобарный процесс, вытекает известное уравнение Майера. Так как dq=c_p·dT=c_v·dT+dl=c_v·dT+R·dT, то R=c_p-c_v.

Используя выражение (4.5), можно показать, что в изобарном процессе энтропия газа

(4.11)

4.2.3.Изотермический процесс (T=const)

В p-v координатах график процесса изображается равнобокой гиперболой (рис. 4.3). Изотермический процесс может протекать как с увеличением объёма (процесс 1-2), так и с уменьшением объёма (процесс 1-2’).

Рис. 4.3. График изотермического процесса в p-v координатах

Запишем для точек 1 и 2 уравнения состояния p₁·v₁=R·T; p₂·v₂=R·T. Следовательно, для изотермического процесса p₁·v₁=p₂·v₂=const.

Приращение внутренней энергии газа

 

Работа газа

(4.12)

 

Теплота, подводимая в процессе

(4.13)

 

Изменение энтальпии газа Δi=Δu+Δ(p·v)=0.

Изменение энтропии газа

(4.14)