Крайова та гвинтова дислокації. Вектор Бюргерса.
Дослідження пружних та пластичних властивостей кристалів привело до несподіваного результату. Теоретично обраховані границі пружності кристалів часто на кілька порядків (102-104) перевищують значення, які спостерігаються на експерименті. Винятком виявилися монокристали особливої форми – так звані вуса. У них теоретичні і експериментальні значення границі пружності практично співпадали. Чим же принципово відрізняється звичайний об’ємний кристал від вусів? Дані електронної мікроскопії та рентгеноструктурні дослідження показали наявність у монокристалах блочної структури. Осі окремих блоків дещо зміщені одна відносно одної на кути від десятої до кількох хвилин. Це призводило до розмитості дифракційної картини у монокристалах.
Дислокації впливають не тільки на механічні властивості кристалів, а й на їх електроопір, оптичні, магнітні властивості, визначають характер росту деяких кристалів.
Розглянемо спочатку крайову дислокацію. Якщо одна із кристалографічних площин уривається в середині кристалу, то обірваний край цієї площини утворює крайову дислокацію. Лінія дислокації позначається ось таким знаком і направлена перпендикулярно площині малюнка. Дислокація може йти досить глибоко у кристалі – на десятки, а то й сотні атомних шарів. Поблизу лінії дислокації кристал найбільше деформований, далі від неї кристалічна структура відновлюється. Саме крайова дислокація відповідає за пластичні властивості кристалів. Пластична деформація кристалів зазвичай пов’язана із таким колективним зміщенням атомів, що його можна розглядати як рух дислокації. Причому цей рух може відбуватися як вздовж лінії дислокації, так і впоперек її.
В ідеальному кристалі завжди можна із векторів трансляції утворити замкнутий контур. Якщо такий контур (його ще називають контуром Бюргерса) побудувати навколо лінії дислокації у дефектному кристалі, такий контур виявиться розірваним. Це контури ABCDEF на рисунках для крайової та гвинтової дислокацій. Вектор Характер дислокації визначається величиною і напрямком вектора Бюргерса. У випадку крайової дислокації довжина вектора Бюргерса відповідає додатковій міжплощинній відстані, пов’язаною із зайвою площиною, і він направлений перпендикулярно лінії дислокації. У випадку ж гвинтової дислокації довжина вектора Бюргерса дорівнює кроку гвинта, тобто міжплощинній відстані, а напрямок паралельний лінії дислокації. В загальному випадку лінія дислокації може являти собою довільну плоску або просторову криву, вздовж якої вектор Бюргерса буде залишатися сталим. Крім того, дислокації можуть розгалужуватись, або виходити на поверхню. Для розгалуження дислокацій існує теорема, аналогічна теоремі Кірхгофа для розгалуження ліній струму. Якщо взяти всі дислокації, що перетинаються в одній точці, то сума їх векторів Бюргерса повинна дорівнювати нулю Те, що дислокації розгалужуються, приводить нас до думки, про оцінку їх кількості у кристалі. Густина дислокацій визначається як кількість дислокаційних ліній, що перетинають одиничну площу всередині кристалу. Можливі значення густини дислокацій змінюються від 102-103 см-2 у найбільш досконалих монокристалах германію і кремнію до 1011-1012 см-2 у сильно деформованих металічних кристалах. Що ще треба додати про дислокації. Поки що ми розглянули, як вони погіршують властивості кристала. Але виявляється, що від дислокацій є користь, та ще й чимала. При вирощуванні кристалів йоду було встановлено, що найменша швидкість росту кристала перевищує передбачену теоретично у Із дуже пересичених розчинів можна вирощувати вуса, про які ми вже згадували. Вважається, що вони мають не більше однієї гвинтової дислокації, вздовж якої вони виросли. Наявність такої дислокації, як і її відсутність, не впливає на міцність такого кристалу. Пластичні деформації (тобто, зсув) та розтягування на таку дислокацію не впливають. Розраховані пружні властивості вусів добро узгоджуються з експериментом.
|

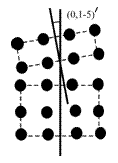 Саме з наявністю блочної структури у кристалах і пов’язали розбіжність теоретичного і експериментального значень границі пружності. У вусах така блочна структура відсутня, отже це і пояснює співпадіння в них експериментального і теоретичного значення границі пружності. Причиною виникнення блочної структури монокристалів є лінійний дефект, який називається дислокацією.
Саме з наявністю блочної структури у кристалах і пов’язали розбіжність теоретичного і експериментального значень границі пружності. У вусах така блочна структура відсутня, отже це і пояснює співпадіння в них експериментального і теоретичного значення границі пружності. Причиною виникнення блочної структури монокристалів є лінійний дефект, який називається дислокацією.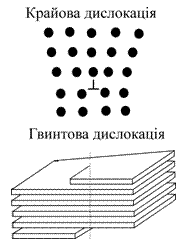 Основними типами дислокацій є крайові та гвинтові дислокації.
Основними типами дислокацій є крайові та гвинтові дислокації.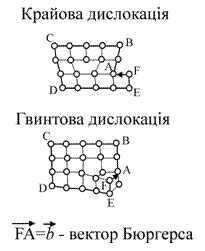 Інший простий тип дислокації – це гвинтова дислокація. Гвинтову дислокацію можна наочно уявити собі, якщо розрізати кристалічну гратку по півплощині і зсунути зовнішні края гратки на відстань, що дорівнює відстані між атомними площинами. У випадку гвинтової дислокації жодна атомна площина не закінчується всередині кристалу. Самі атомні площини практично паралельні і з’єднуються між собою таким чином, що фактично кристал складається із єдиної атомної площини, закрученої гвинтом. На кожному обороті площа піднімається на одну міжплощинну відстань. Лінія гвинтової дислокації проходить через вісь гвинта.
Інший простий тип дислокації – це гвинтова дислокація. Гвинтову дислокацію можна наочно уявити собі, якщо розрізати кристалічну гратку по півплощині і зсунути зовнішні края гратки на відстань, що дорівнює відстані між атомними площинами. У випадку гвинтової дислокації жодна атомна площина не закінчується всередині кристалу. Самі атомні площини практично паралельні і з’єднуються між собою таким чином, що фактично кристал складається із єдиної атомної площини, закрученої гвинтом. На кожному обороті площа піднімається на одну міжплощинну відстань. Лінія гвинтової дислокації проходить через вісь гвинта.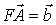 , або його позначають
, або його позначають  , який необхідно провести для того, щоб замкнути кінці контура Бюргерса, називається вектором Бюргерса даної дислокації.
, який необхідно провести для того, щоб замкнути кінці контура Бюргерса, називається вектором Бюргерса даної дислокації.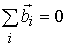 .
. разів. Головною проблемою при вирощуванні кристалів є створення на поверхні кристалу зародку наступного шару, якщо поверхня кристалу є досконалою. Якщо ж у кристалі є гвинтова дислокація, то у зародку для нового шару немає потреби, кристал буде рости від краю сходинки, причому на досконалості кристалу це ніяк не позначиться. Розрахунки швидкості росту кристалу, що базуються на цьому механізмові, добре узгоджуються із експериментом.
разів. Головною проблемою при вирощуванні кристалів є створення на поверхні кристалу зародку наступного шару, якщо поверхня кристалу є досконалою. Якщо ж у кристалі є гвинтова дислокація, то у зародку для нового шару немає потреби, кристал буде рости від краю сходинки, причому на досконалості кристалу це ніяк не позначиться. Розрахунки швидкості росту кристалу, що базуються на цьому механізмові, добре узгоджуються із експериментом.


