Індекси Міллера.
Транслюючи атомну площину на вектор трансляції, що не лежить у цій площині, ми отримаємо всю кристалічну гратку. Із трансляційної симетрії кристалу випливає, що ми отримаємо нескінченну кількість атомних площин, паралельних вибраній. Множина паралельних рівновіддалених атомних площин називається сімейством атомних площин.
Давайте розглянемо визначення площин на прикладі кубічного кристалу, оскільки зручніше працювати з декартовою системою координат. Як ми вже зазначали, будь-який кубічний кристал обов'язково має три осі симетрії третього порядку. Осі координат направляють уздовж ребер куба, об'ємні діагоналі якого є осями симетрії третього порядку. На рисунку показані такі осі координат і розташовані на них атоми. Позначимо відстань між найближчими атомами на осі 0 x через a. Оскільки кристал має вісь симетрії третього порядку, то такої ж відстані між найближчими атомами і на осях 0 y і 0 z. Приймемо a за одиницю виміру. Нехай якась площина проходить через три атоми на осях координат і відтинає на них три відрізки sxa, sya і sza. Величини sx, sy і sz, природно, – цілі числа, причому можуть бути як додатними, так і від’ємними. Рівняння площини, яка не паралельна жодній з координатних осей, має вигляд Вона відтинає на осях відрізки Тоді рівняння площини можна записати у вигляді Це канонічне рівняння площини. Складемо відношення обернених величин відтятих відрізків і виразимо його через відношення таких трьох найменших цілих чисел h, k і l, що Наведемо конкретні приклади. 1. Нехай sx =2, sy =3 і sz =1, як це показано на рисунку. Тоді 2. Тепер визначимо індекси Міллера для затемненої площини на другому рисунку. Вона перетинає вісь 3. Затемнена площина на наступному рисунку має міллеровські індекси (111), тобто 4. Цікавим є наступний випадок. Зверніть увагу. А тепер як розв’язати зворотну задачу – відтворити площину за її індексами Міллера? Для того щоб за індексами Міллера (h k l) побудувати обумовлену ними площину досить на осях координат відкласти відрізки Тепер підкреслимо важливу обставину. Очевидно, що одна трійка індексів Міллера визначають не одну атомну площину, а ціле сімейство паралельних площин Симетрія може привести до існування декількох сімейств площин, фізичні властивості яких однакові.Наприклад, у кубічному кристалі в площин (100), (010), (001) ( Анізотропія кристалів має на увазі, що їхні властивості відрізняються у різних напрямках. Ці напрямки також треба задавати. Вектор, що з'єднує початок координат з яким-небудь атомом, можна записати як У кубічних кристалах напрямок [ uvw ] перпендикулярний площині (uvw). У кристалах з більш низькою симетрією це звичайно не так. У гексагональних кристалах вводять чотири індекси Міллера. Три координатні осі направляють у площині основи під кутом 120°, а четверту - вздовж осі симетрії 6 порядку. Для виділених граней індекси Міллера:
Зверніть увагу, сума перших трьох індексів у гексагональній системі дорівнює нулю. Це є наслідком того, що геометрична сума векторів-ортів у цій площині дорівнює нулю (показати). Отже, у гексагональній структурі не може бути таких площин, як
|

 Вам добре відомо із курсу аналітичної геометрії, що через три точки, які не лежать на одній прямій, можна провести площину. Площина в кристалі, у якій знаходяться, принаймні, три його атоми, називається атомною площиною кристалу. Очевидно, що вектори, проведені між цими атомами, є векторами ґраток. Отже, трансляцією на ці вектори ми можемо розмножити число атомів на цій площині. Тому атомна площина ідеального (а, отже, нескінченного кристала) містить нескінченне число атомів.
Вам добре відомо із курсу аналітичної геометрії, що через три точки, які не лежать на одній прямій, можна провести площину. Площина в кристалі, у якій знаходяться, принаймні, три його атоми, називається атомною площиною кристалу. Очевидно, що вектори, проведені між цими атомами, є векторами ґраток. Отже, трансляцією на ці вектори ми можемо розмножити число атомів на цій площині. Тому атомна площина ідеального (а, отже, нескінченного кристала) містить нескінченне число атомів. Анізотропія кристалів, тобто відмінність їх фізичних властивостей у різних кристалографічних напрямках, приводить до того, що різні атомні площини кристала мають різні властивості. Як можна задати розташування різних атомних площин у кристалічній ґратці? Очевидно, для цього потрібно вибрати систему координат і одиниці виміру по осях координат. Виділеними напрямками в кристалі є його осі симетрії. Тому зручним і природним є вибрати напрямок осей координат уздовж осей симетрії кристала.
Анізотропія кристалів, тобто відмінність їх фізичних властивостей у різних кристалографічних напрямках, приводить до того, що різні атомні площини кристала мають різні властивості. Як можна задати розташування різних атомних площин у кристалічній ґратці? Очевидно, для цього потрібно вибрати систему координат і одиниці виміру по осях координат. Виділеними напрямками в кристалі є його осі симетрії. Тому зручним і природним є вибрати напрямок осей координат уздовж осей симетрії кристала. .
. , де
, де  .
. .
.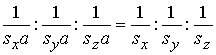
 . Числа h, k і l називають індексами Міллера. Прийнято записувати їх у круглих дужках (h k l). Вони задають розташування розглянутої площини.
. Числа h, k і l називають індексами Міллера. Прийнято записувати їх у круглих дужках (h k l). Вони задають розташування розглянутої площини. і (h k l) = (326).
і (h k l) = (326). і паралельна осям
і паралельна осям  та
та  . Паралельність еквівалентна тому, що вони перетинаються на нескінченності, отже
. Паралельність еквівалентна тому, що вони перетинаються на нескінченності, отже  і (hkl)=(100).
і (hkl)=(100). .
. . Індекси Міллера такої площини мають вигляд (
. Індекси Міллера такої площини мають вигляд ( 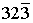 ). В останньому випадку
). В останньому випадку  означає мінус три і відповідає перетину площиною осі 0 z на її від’ємній частині.
означає мінус три і відповідає перетину площиною осі 0 z на її від’ємній частині. ,
,  і
і 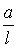 , а потім через їхні кінці провести шукану площину. Наприклад, нехай індекси Міллера (hkl)=(112). Записуємо співвідношення
, а потім через їхні кінці провести шукану площину. Наприклад, нехай індекси Міллера (hkl)=(112). Записуємо співвідношення  , вважаючи відрізок
, вважаючи відрізок  одиничним. Будуємо відрізки на осях та по них проводимо площину, як на останньому рисунку.
одиничним. Будуємо відрізки на осях та по них проводимо площину, як на останньому рисунку.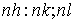 . Властивості всіх цих площин однакові.
. Властивості всіх цих площин однакові. 00), (0
00), (0  , де
, де  ,
,  і
і  є цілі числа. Вони задають напрямок вектора ґратки. Для визначення напрямку вектора досить знать відношення
є цілі числа. Вони задають напрямок вектора ґратки. Для визначення напрямку вектора досить знать відношення  . Це дозволяє для виконання цієї задачі задавати три таких мінімальних числа u, v і w, що задовольняють співвідношенню
. Це дозволяє для виконання цієї задачі задавати три таких мінімальних числа u, v і w, що задовольняють співвідношенню  . При позначенні напрямку ці числа беруть у квадратні дужки [ uvw ]. Сукупність усіх фізично еквівалентних напрямків позначають
. При позначенні напрямку ці числа беруть у квадратні дужки [ uvw ]. Сукупність усіх фізично еквівалентних напрямків позначають 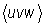 . У кубічних кристалах такими є, наприклад, напрямок
. У кубічних кристалах такими є, наприклад, напрямок  , тобто [100], [010], [001], [
, тобто [100], [010], [001], [ 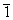 , як і раніше, означає мінус одиницю.
, як і раніше, означає мінус одиницю.


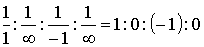
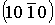
 , або
, або  .
.


