Уравнение линейной регрессии
Это означает построение уравнения y = b0 + b1x1 + b2x2 +... + bmxm, (2) которое называется уравнением линейной регрессии. При подстановке в это уравнение значений факторных переменных i -го наблюдения получим величину yi = b0 + b1xi1 + b2xi2 +... + bmxim, (3) которая не будет совпадать с наблюдаемым значением yi. Разность между наблюдаемым значением yi и значением, рассчитанным по уравнению регрессии, называется остатком в наблюдении i и обозначается ei: ei=yi – Используя соотношение (4), наблюдаемые значения yi можно представить как yi = При построении нормальной линейной модели множественной регрессии учитываются пять условий: 1) факторные переменные x1i…xmi – неслучайные или детерминированные величины, которые не зависят от распределения случайной ошибки модели регрессии bi; 2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях: 3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений: 4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т.е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):
5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией.
|

 . (4)
. (4) ,
, 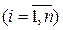 ;
; ;
; , (i ≠ j);
, (i ≠ j);


