Методы устранения мультиколлинеарности
К основным способам устранения мультиколлинеарности в модели множественной регрессии относятся: 1) один из наиболее простых способов устранения мультиколлинеарности состоит в получении дополнительных данных. Однако на практике в некоторых случаях реализация данного метода может быть весьма затруднительна; 2) способ преобразования переменных, например, вместо значений всех переменных, участвующих в модели (и результативной в том числе) можно взять их логарифмы: ln y = b0+b1ln x1+b2ln x2+e. Однако данный способ также не способен гарантировать полного устранения мультиколлинеарности факторов; Если ни одну из факторных переменных, включённых в модель множественной регрессии, исключить нельзя, то применяют один из основных смещённых методов оценки коэффициентов модели регрессии – гребневую регрессию или ридж (ridge). При использовании метода гребневой регрессии ко всем диагональным элементам матрицы (ХТХ) добавляется небольшое число τ;: 10-6 ‹ τ; ‹ 0,1. Оценивание неизвестных параметров модели множественной регрессии осуществляется по формуле:
где In – единичная матрица. Результатом применения гребневой регрессии является уменьшение стандартных ошибок коэффициентов модели множественной регрессии по причине их стабилизации к определённому числу. Метод главных компонент является одним из основных методов исключения переменных из модели множественной регрессии.
|

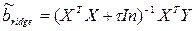 ,
,


