Матричный вид уравнения линейной регрессии

Представим выборочные данные в виде матрицы-столбца Y значений зависимой переменной и матрицы X значений объясняющих переменных, коэффициенты уравнения регрессии – в виде матрицы-столбца B, а остатки наблюдений – в виде матрицы-столбца E:

, , ,

Используя введенные обозначения, соотношение (5) можно записать в матричном виде:

Y = XB + E. (6)

Для определения коэффициентов регрессии b₀, b₁,..., b_m используется метод наименьших квадратов (МНК).

Условия построения нормальной линейной модели множественной регрессии, записанные в матричной форме:

1) факторные переменные x_1j…x_mj – неслучайные или детерминированные величины, которые не зависят от распределения случайной ошибки модели регрессии e_i;

2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях: , ;

3) предположения о том, что дисперсия случайной ошибки модели регрессии является постоянной для всех наблюдений и ковариация случайных ошибок любых двух разных наблюдений равна нулю, записываются с помощью ковариационной матрицы случайных ошибок нормальной линейной модели множественной регрессии:

,

где G² – дисперсия случайной ошибки модели регрессии е;

In – единичная матрица размерности (n*n).

4) случайная ошибка модели регрессии ε является независимой и независящей от матрицы Х случайной величиной, подчиняющейся многомерному нормальному закону распределения с нулевым математическим ожиданием и дисперсией G²: е→N(0;G²In).

В нормальную линейную модель множественной регрессии должны входить факторные переменные, удовлетворяющие следующим условиям:

1) данные переменные должны быть количественно измеримыми;

2) каждая факторная переменная должна достаточно тесно коррелировать с результативной переменной;

3) факторные переменные не должны сильно коррелировать друг с другом или находиться в строгой функциональной зависимости.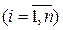